Download Introductory Course to Matlab with Financial Case Studies
Transcript
University of Cyprus
Public Business Administration Department
Introductory Course to
Matlab with Financial Case
Studies
Panayiotis Andreou
P repared by:
PhD Candidate
PBA – UCY
Lefkosia, September 2003
Table of Contents
1. Introduction.......................................................................................3
1.1 Learning Matlab ............................................................................3
1.2 Basic Definitions............................................................................6
1.3 Information of How to Read This Handout........................................8
1.4 Starting Up Matlab ........................................................................9
1.5 Matlab’s Windows ..........................................................................9
1.5.1 Command Window – Matlab as a Calculator .............................12
1.5.1.1 Controlling Command Window Input and Output ................17
The format function:.................................................................18
Suppressing Output .................................................................19
Entering Long Statements .........................................................19
Command Line Editing .............................................................20
Interrupting a Command, a Script or a Function .........................20
Current Directory.....................................................................20
1.5.2 Editor/Debugger....................................................................21
1.4.3 Help Options..........................................................................22
he l p Command............................................................................22
l ookfor Command........................................................................23
The Help Window/Browser...........................................................23
2. Manipulating Vectors and Matrices ....................................................25
2.1 Row Vectors ................................................................................25
2.1.1 The Colon Notation.................................................................27
2.1.2 Column Vectors .....................................................................29
2.1.3 Transporting Vectors ..............................................................30
2.1.4 Vector Manipulations Related to Products, Division, and Powers.31
2.1.4.1 Scalar Product .................................................................31
2.1.4.2 Dot Product .....................................................................32
2.1.4.3 Dot Division and Power.....................................................33
2.1.4.3 Some Useful Vector Functions ...........................................36
2.2 Two Dimensional Arrays (Matrices)................................................37
2.2.1 Transpose of a Matrix.............................................................39
2.2.2 Elaborating on Parts of Matrices – The Colon Notation...............40
2.2.2 Matrix Basic Manipulations.....................................................44
2.1.4 Matrix Manipulations Related to Products, Division, and Powers 44
2.1.4.1 Matrix Dot Product, Division and Powers ............................44
2.1.4.2 Matrix to Vector Product – Matrix to Matrix Product ............45
2.1.5 Special Cases of Matrices........................................................47
2.1.5 Additional Useful Matrix Functions ..........................................48
2.1.6 Example: System of Linear Equations ......................................48
3. Plots and Graphs (2D and 3D) ...........................................................51
3.1 Creating 2D Line Plots..................................................................51
3.1.1 Plot Edit Mode .......................................................................52
3.1.2 Functions and Style Facilities Related to Plots...........................53
1
3.2 Creating 3D Graphs.....................................................................59
3.2.1 Creation of 3D Line Plots ........................................................59
3.2.2 Creation of 3D Mesh and Surface Graphs.................................59
3.2.2.1 Examination of a Function’s Critical Points.........................65
4. Control Flow ....................................................................................68
4.1. Logical and Relational Operators..................................................68
4.1.1 The any and al l Functions.......................................................70
4.2. Conditional Statements ...............................................................71
4.2.1 The i f Statement.....................................................................72
4.2.2 The swi tch Statement .............................................................73
4.3. Loop Expressions........................................................................73
4.3.1. The for Loop..........................................................................74
4.3.2. The while Loop......................................................................74
4.3.3. Nested Conditional and Loop Expressions................................75
4.3.4. Additional Control Flow Statements ........................................75
5. m-files: Scripts and Functions ...........................................................77
5.1 m-files: Functions ........................................................................77
5.1.1 Basic Parts of a Function ........................................................79
5.1.1.1 Function Definition Line....................................................79
5.1.1.2 The H1 Line .....................................................................81
5.1.1.3 The Help Text ...................................................................81
5.1.1.4 The Body Text ..................................................................82
5.2 Scripts........................................................................................82
6. Cells and Structures.........................................................................85
6.1 Cells ...........................................................................................85
Cell indexing..................................................................................86
Content indexing............................................................................87
6.2 Structures...................................................................................89
Building structure arrays using assignment statements.....................90
Building structure arrays using the struct function ...........................91
7. Entering and Saving Data Files..........................................................94
7.1. Reading Text ASCII Files: The load command ................................94
7.2 Saving Text ASCII Files: The save command ...................................96
7.3 Other Reading and saving commands............................................97
8. Case Studies....................................................................................98
8.1 The Black – Scholes- Merton Options Pricing Formula.....................98
8.1.1 Implementation of the BSM Formula........................................99
8.1.2 BSM Derivatives................................................................... 101
8.1.3 BSM Plots and Surfaces........................................................ 102
8.1.4 BSM Implied Volatility .......................................................... 102
8.2 Function Minimization and Plots................................................. 105
8.3 Portfolio Optimization................................................................. 112
References......................................................................................... 118
2
First Section
1. Introduction
This handout demonstrates a comprehensive introduction to the basic
utilities of a high technical programming language encapsulated under the
computing environment of Matlab. It was prepared based on version 6.5
Release 13, but since it does not have many differences from previous ones,
it can also operate for older versions as well. Upon reading it, you will be in
a position to create programming code to solve elementary (or even
intermediate) financial problems. It has been prepared for postgraduate
students registered for the Master in Finance program offered by the
Department of Business and Public administration – University of Cyprus.
1.1 Learning Matlab
Matlab (the name stands for: Matrix Laboratory) is a high performance
programming language and a computing environment that uses vectors and
matrices as one of its basic data types (MATLAB® is a registered trademark
of the MathWorks, Inc.). It is a powerful tool for mathematical and technical
calculations and it can also be used for creating various types of plots. It
performs the basic functions of a programmable calculator whereas someone
can write, run/execute and save a bundle of commands. In the last few
years, Matlab has become very popular because it enables numerous ways
to solve various problems numerically via a user-friendly programming
language. It is particularly easy to generate a programming code, execute it
to get the desire solution, draw some relevant graphs and look at the
interesting features of the problem under consideration. What makes Matlab
so convenient to many fields (including finance) is that it integrates
computation, visualization and programming in an easy to use environment.
Just for historical purposes, the first version of Matlab was written in 1970s
by a numerical analyst names Cleve Moler, and since then has become a
successful retail product.
3
Matlab features a family of add-on application-specific solutions called
toolboxes. A toolbox is a comprehensive collection of Matlab functions (Mfiles) that extend the Matlab environment to solve particular classes of
problems. For example, the Financial Toolbox includes ready to use
functions that provide a complete integrated computing environment for
financial analysis and engineering. The toolbox has everything you need to
perform mathematical and statistical analysis of financial data and display
the results with presentation-quality graphics. With MATLAB and the
Financial Toolbox, you can: compute and analyze prices, yields, and
sensitivities for derivatives and other securities, and for portfolios of
securities; analyze or manage portfolios; design and evaluate hedging
strategies and many more.
This handout is about a brief introductory course in the most important
parts of Matlab. After finishing this, you will be able to:
i.
Utilize the basic mathematical operations;
ii.
Get know the general purpose commands of Matlab;
iii.
Become familiar with some of the elementary functions, matrix
and numerical linear algebra functions, as well as some graphic
and plot commands;
iv.
Manipulate matrices (i.e. create and edit vectors and matrices,
build a larger matrix from a smaller one, etc);
v.
Learn how to use the relational operators (<, >, <=, >=, ==, ~=) and
logical operators (& AND, | OR, ~ NOT);
vi.
Recognize built in variables, define new ones and performing
computations with them;
vii.
Learn how to use if and switch statements;
viii.
Learn how to correctly utilize loop commands, such as the for loop,
and the while loop;
ix.
Write and edit your own m-files and functions for solving a specific
problem;
x.
…Numerous other utilities and uses depending on your will to learn
and utilize this technical language.
4
It is better to use this handout in direct use with the Matlab. It will be more
beneficial if while reading these notes you sit in front of a PC and type the
various commands and execute the given examples.
Although the Matlab package includes extensive help facilities that can be
viewed via a very user-friendly Help Browser, if it is needed, you can also
find additional online (through Internet) help at the following electronic
address:
http://www.mathworks.com/access/helpdesk/help/helpdesk.shtml
or at:
http://wwwhost.cc.utexas.edu/math/Matlab/Manual/ReferenceTOC.html
Moreover, various download, trials and the Matlab Central File Exchange
that contains hundreds of files contributed by users and developers
of Matlab and related products can be found at:
http://www.mathworks.com/web_downloads/
Additionally, any functions that have been created for examples and all
those that are needed to work with the case studies are located in the folder
named as: Matlab Examples (for further details send me an email or ask
during the class).
Lastly, I will appreciate to send me feedback information concerning these
notes related with spelling errors, sections that should be clarified or
explained better (or even added) and any other that can contribute to the
improvement of this handout. The email address that you can reach me is:
benjamin@avacom.net.
5
1.2 Basic Definitions
Before moving to the introduction of issues specific to Matlab, some very
basic definitions on computers and programming should be set forth. These
include:
General [1]
•
bit (short for binary digit) is the smallest unit of information on a
computer. A single bit can hold only one of two values: 0 or 1. More
meaningful information is obtained by combining consecutive bits
into larger units, such as byte.
•
byte consists a unit of 8 bits and is capable to hold a single character.
Large amounts of memory are indicated in terms of kilobytes (1024
bytes), megabytes (1024 kilobytes), and gigabytes (1024 megabytes).
•
data is information represented with symbols such as numbers,
words, images, etc.
•
command is a collection of programming words that instruct the
computer to do a specific task.
•
algorithm is a set of commands that aim to solve a predetermined
problem.
•
program is the implementation of the algorithm suitable for
execution by a computer.
•
variable is a container that can hold a value. For example, in the
expression: z+a, both z and a are variables. Variables can hold both
numerical data (e.g. 10, 98.5) and characters or strings (e.g. 'd' or
'pba').
•
constant is a value that never changes. It can be a numeric, a
character or a string.
•
bug is an error in a program, causing the program to stop running,
not to run at all or to provide wrong results. Some bugs can be very
subtle and hard to find. The process of finding and removing the bugs
is called debugging.
Matlab Specific [2]
•
workspace is the memory allocated to Matlab and is used to
temporarily store variables.
6
•
m-file is a file that contains Matlab’s language code. m-files can be
functions that accept arguments and produce output, or they can be
scripts that execute a series of Matlab statements. For Matlab to
recognize a file as an m-file, its file name extension must be *.m.
•
functions are m-files that can accept input arguments and return
output arguments. The name of the m-file and the calling syntax
name of the function should be the same. Functions operate on
variables within their own workspace, separate from the workspace
you access at the Matlab command prompt. Functions are useful for
extending the existing Matlab language for personal applications (e.g.
create a function that returns the expected return and standard
deviation related with a set of companies).
•
scripts can operate on existing data in the workspace, or they can
create new data on which to operate. Although scripts do not return
output arguments, any variables that they create remain in the
workspace, to be used in subsequent computations. In addition,
scripts can produce graphical output using functions. Scripts are
useful for automating a series of steps that are needed to be
performed many times (e.g. to create a script that executes a series of
functions related to portfolio optimization).
•
Every variable has a name and a data type. With Matlab, accepted
variables names do not start with symbols (like ~, +, -) or numbers,
use lower and upper case letters do not exceed 63 characters and do
not resemble reserved words and build-in functions. Acceptable
definitions include: Time, x, y, XYZ, Ray_value, U3e23 etc. Nonacceptable definitions are the followings: +Time, 3587num, _XYZ,
rayX-values, for, end, while, case, day etc. The data type is a
classification of particular type information. Among the most usable
types are: integer a whole number, a number without any fraction
(e.g. 12, 10, 89); floating point a number with a fractional part (e.g.
25.7, 78,1, 0.000005, 5e-5 which is equal to 5*10-5); and character
readable text character (e.g. 'k'). With Matlab, it is not need to type or
declare variables used in the m-files. Any operation that assigns a
value to a variable creates the variable, if needed, or overwrites its
current value, if it already exists.
7
•
Every build in or user made function has a calling syntax that is
unique for each function. In Matlab, to call a function you type the
function’s name and you enclose the input arguments in brackets (if
more than one input argument exist, then commas should be used to
separate the expressions).
•
Matlab is handled through the use of various windows, that each is
related with a certain utility. For example, the Command Window is
used to enter variables and run functions and m-files, the Command
History Window makes a diary with the commands that you have
recently entered in the command window, the Workspace Browser
allows you to view the variables that are stored in the workspace, etc.
Any reference to such windows that is made in the main body of
these notes will be explained in detail if it is needed.
1.3 Information of How to Read This Handout
In the main body of this handout, words that refer to a keyboard instruction
will be written in brackets and in boldface letter. For example, [Enter] will
represent one key-press of the Enter button of the keyboard. Words that
represent Matlab’s reserved words such as for, end, who, etc, words that
imply a Matlab term such as m-file, script, function, etc, or key-words related
with the interface menu and toolbars will appear in italics. Words in the
main body that refer to Matlab’s vector and matrix names, Matlab’s build in
functions or user’s new functions will be presented with a shadow style. For
example, if in the main body a reference is made to a vector saved in the
workspace with the name “Hours” it will look like: Hours. The reference to
Matlab’s function that creates 2D figures will be as: pl ot. Moreover, note that
although each function has a specific calling syntax, usually only the name of
the function will be displayed; if not presented in the body text of this
handout, the user should be responsible to find the exact calling syntax of
the function via the Matlab’s help facilities.
Other Matlab output such as warnings, tips or Matlab commands will be
enclosed in double quote marks “ ”. The definition of Matlab related words
and expression in windows (as you will see later) consist exceptions from
these rules. Lastly, references to books and other reading material are
8
numbered in square brackets (e.g. [2] is the Matlab online help facilities; see
the section with the references). Additionally, if a figure or a table heading
that has a superscript number enclosed in square brackets will indicate the
source from where it was copied (for instance, Figure[2] X: Figure heading,
indicates
that the current figure was copied from Matlab online help
facilities).
1.4 Starting Up Matlab
The following instructions help for starting up the Matlab in the Economics
and Business Computer Lab:
Step #1: Use the [Ctrl]+[Alt]+[Del] combination to bring up the
logon screen (at this point you should enter the user name and
your password and after to press [Enter])
Step #2: After few seconds, you view the PC’s Desktop screen with
all available icons. Find the Matlab’s shortcut icon (labeled as
“Matlab” and looks like
) and double click on it. After few
moments, the Matlab starts up and the following sentence appear
in one of the screens:
“To get started, select "MATLAB Help" from the Help menu”
Step #3: The Matlab is now ready to be used (if you want to quit
Matlab, from the window named as Command Window either type
qui t or exit from the toolbar choose: File > Exit Matlab).
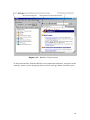
1.5 Matlab’s Windows
When you start up Matlab, you will view the following interface (Figure 1 – a
difference interface may appear if someone before you has changed the
active windows from the View menu):
9
Figure[2] 1: The Matlab desktop
The above is termed as the Matlab Desktop (graphical user interfaces) and
contains tools for managing files, variables, and applications associated with
Matlab. Think of the desktop as your instrument panel for Matlab. The
toolbar in the Matlab desktop provides easy access to frequently used
operations. Hold the cursor over a button and a tooltip appears describing
the item. Note that some of the tools also have toolba rs within their windows
[2].
You can change the way your desktop looks by opening, closing, moving,
and resizing the tools in it. Use the View menu to open or close the tools.
You can also move tools outside the desktop or move them back into the
desktop (docking). All the desktop tools provide common features such as
context menus and keyboard shortcuts. You can specify certain
characteristics for the desktop tools by selecting Preferences from the File
menu. For example, you can specify the font characteristics for command
10
window text. For more information, click the Help button in the Preferences
dialog box [2].
Additionally, two more windows that can be seen in Figure 1 can help the
user during the programming time. The first one and most important is the
workspace browser (Figure 2). The Matlab workspace consists of the set of
variables (named arrays) built up during a Matlab session and stored in
memory. You add variables to the workspace by using functions, running mfiles, and loading saved workspaces.
Figure[2] 2: The Matlab Workspace Browser
The workspace is not maintained after you end the Matlab session. To save
the workspace to a file that can be read during a later Matlab session, select
Save Workspace As from the File menu.
Another useful window, is the command history (Figure 3). Statements you
enter in the Command Window are logged in the Command History. In the
Command History, you can view previously run statements, and copy and
execute selected statements.
11
Select one or more lines
and right -click to copy
and re-use the command
with the command
window, to evaluate it or
to create an m-file
Figure 3: The Matlab Command Window
To activate or close these and some other windows, choose View from the
toolbar. In the following few subsections, the most basic from this screen are
documented.
1.5.1 Command Window – Matlab as a Calculator
It is the main window in which the user communicates with the software. In
the command window, the user can view the prompt symbol “>>” which
indicates that Matlab is ready to accept various commands by the user. Via
this window, the user can employ the basic arithmetic operators like: “+”
(addition), “-” (subtraction), “*” (multiplication), “/” (division), “^” (powers)
and the “( )” (brackets), as well as many other build in elementary and other
functions and commands that will be referred to later.
As a first example, enter the following command that performs a basic
calculation (Figure 4):
“5+6/12+9/3-21”
12
Figure 4: A basic calculation
The Matlab displays the results into a variable named as ans. This is a
default variable name that is used by the command window to display the
most recent results instructed by the user that has not defined a specific
name. Continue by entering the following command that creates a fourelement vector (Figure 5):
“[1 2 3 4]”
Figure 5: A four-element vector
13
The square brackets “[ ]” indicate the definition of the vector. Also, the space
between the vector numbers separates the vector’s elements. The comma “,”
is another way of separating the elements. Additionally, note that the default
variable ans has lost its previous value in order to store the results of the
most recent operation.
As another example, enter the following command that creates a 3-by-3
magic square saved in the matrix variable M:
“M=magi c(3)”
and after pressing [Enter] you get the Matlab’s result (Figure 6):
Figure 6: A 3-by-3 magic table
The magic square is created using the element function magi c that is
already built in Matlab.
14
Type also the following:
“x=[(2^2+1)^2-15/4*6.1, 1.23e-2]”
and after pressing [Enter] you get the Matlab’s result (Figure 7)
Figure 7: A 2-element vector
Observe that the very first command that you have entered in the command
window has vanished with the additional of the last one (of course it
depends on the size of the window, in here the command window is
minimized so earlier commands vanish too quickly). You can use the scroll
bar on the right to navigate the command window and go up to see the
earlier commands (or view them via the command history window).
Matlab calculates the quantities as follows:
•
First come the quantities in brackets
•
Power calculation follow: (e.g. 5 + 2^2 = 5 +4 = 9)
15
•
“*” and “/” follow by working from left to right: (e.g. 2*8/4 = 16/4 = 4)
•
“+” and “-” follow last, from left to right: (e.g. 6-7+2= -1+2 = 1)
Note that “e” notation is used for very large or ve ry small numbers. By
definition: 1e1=1X101 and 1e-1=1X10-1.
Trigonometric
Exponential
s in
s i nh
as i n
as i n h
cos
cos h
acos
acos h
t an
t an h
at an
Sine.
Hyperbolic sine.
Inverse sine.
Inverse hyperbolic sine.
Cosine.
Hyperbolic cosine.
Inverse cosine.
Inverse hyperbolic cosine.
Tangent.
Hyperbolic tangent.
Inverse tangent.
at an 2
Four quadrant inverse
tangent.
Inverse hyperbolic tangent.
Secant.
at an h
sec
s e ch
as e c
as e ch
cs c
cs ch
acs c
acs ch
cot
Inverse secant.
Inverse hyperbolic secant.
Cosecant.
Hyperbolic cosecant.
Inverse cosecant.
Inverse hyperbolic cosecant.
Cotangent.
conj
i mag
re al
unwrap
i s re al
cpl xpai r
Hyperbolic cotangent.
Inverse cotangent.
Inverse hyperbolic
cotangent.
Hyperbolic cotangent.
Inverse cotangent.
Inverse hyperbolic
cotangent.
cot h
acot
acot h
abs
angl e
compl e x
acot
Exponential
Natural logarithm.
Common (base 10) logarithm.
Base 2 logarithm and dissect floating
Base 2 power and scale floating point
Power that will error out on complex
Natural logarithm of real number.
Square root of number greater than or
Square root.
Next higher power of 2.
Complex
Hyperbolic secant.
cot h
acot h
e xp
Log
l og10
l og2
pow2
re al pow
re al l og
re al s qrt
s qrt
ne xt pow2
Absolute value.
Phase angle.
Construct complex data from real and
imaginary parts
Complex conjugate.
Complex imaginary part.
Complex real part.
Unwrap phase angle.
True for real array.
Sort numbers into complex conjugate pairs
Rounding and Remainder
fi x
Round towards zero.
fl o o r
Round towards minus infinity.
ce i l
round
Round towards plus infinity.
Round towards nearest integer.
mod
Modulus (signed remainder after
re m
s i gn
remainder after division.
Signum.
Table 1: The elementary build-in functions
Matlab can handle three different kinds of numbers: integers, real numbers
and complex numbers (with imaginary parts). Moreover, it can handle nonnumber
expressions
like:
NaN
(Not-a-Number)
produced
from
mathematically undefined operations like: 0/0, ∞ * ∞ and i nf produced by
16
operations like 1/0. Matlab as a calculator includes a variety of build-in
mathematical functions like: trigonometric, exponential, complex, rounding
and remainder, etc. Table 1 below, depicts these elementary mathematical
build-in functions (to learn how to use these commands, review the Matlab
help facilities located in section 1.5.3).
Note the build-in functions exhibited in Table 1 have their own calling syntax.
For example, if you type si n in the command window, Matlab returns the
following error massage:
“??? Error using ==> sin”
“Incorrect number of inputs.”
This happened because the si n function requires an input expression like a
number enclosed in brackets. If you enter:
“si n(5)”
then you get an answer:
“ans =
-0.9589”
In the rest of this handout, only the name of the build in functions will be
given. Beside some exceptions where the correct calling syntax of a function
is fully tabulated, the user is responsible in knowing the necessary input
arguments to the function. Additional the use of the command window will
be apparent as you read this manuscript since the learning of a computer
programming language is pure a “learning by doing” process.
1.5.1.1 Controlling Command Window Input and Output
This section presents ways by which the user can control the command
window input and output.
17
List of Useful Commands:
w ho
Lists current variables located in the workspace.
whos
A long form of who. It lists all the variables in the
current workspace, together with information about their
size, bytes, class, etc.
cl e a r
Clear variables and functions from memory.
home
Moves the cursor to the upper left corner of the command
window and clears the visible portion of the window. Use
the scroll bar to see what was on the screen previously.
cl c
Clears the command window and homes the cursor.
qui t
Terminates Matlab.
The format function:
The format function controls the numeric format of the values displayed by
Matlab. The function affects only how numbers are displayed, not how
Matlab computes or save them. Here are the different formats, together with
the resulting output produced from a vector x with components of different
magnitudes [2]. In the command window type:
“format short”
and afterwards:
“x”
for retrieving the x vector that you have created before to get:
“x =
2.1250
0.0123”
Note that with this format only 4-decimals place are being used (in total 5
digits). Try also the following format commands to see what you get:
format short e
Floating-point format with 5 digits.
format short g
Best of fixed or floating-point format with 5 digits.
18
format l ong e
Floating-point format with 15 digits.
format l ong g
Best of fixed or floating-point format with 15 digits.
format bank
Fixed format for dollars and cents.
Suppressing Output
If you simply type a statement and press [Enter], Matlab automatically
displays the results on screen. However, if you end the line with a semicolon
“;” Matlab performs the computation but does not display any output [2].
This is particularly useful when you generate large matrices. For example,
“A = magi c(100);”
although Matlab creates a 100-by-100 matrix saved in the workspace, the
result is not displayed on the command window. Moreover, when a
command ends with “;”, is allowed to enter additional commands before
pressing the [Enter] key. For instance,
“A = magi c(100); B=A;”
will perform two commands the one after the other. In here, after creating
the 100-by-100 magic square that is stored in the A (matrix) variable, matrix
B is created to hold the same values as with A. Additionally, note that if two
or more statements are separated with commas, Matlab will display the
results in the screen in the order that these statements were entered.
Entering Long Statements
If a statement does not fit on one line, use an ellipsis (three periods), “...”,
followed by [Enter] to indicate that the statement continues on the next line.
For example,
“s = 1 -1/2 + 1/3 -1/4 + 1/5 - 1/6 + 1/7 ...
- 1/8 + 1/9 - 1/10 + 1/11 - 1/12”
to get:
19
“s =
0.65321”
Blank spaces around the “=”, “+”, and “-“operators are optional, but they
improve readability.
Command Line Editing
Various arrow and control keys on your keyboard allow you to recall, edit,
and reuse statements you have typed earlier. For example, suppose you
mistakenly enter:
“rho = (1 + sqt(5))/2”
You have misspelled square root: sqrt. Matlab responds with:
“Undefined function or variable 'sqt'”
Instead of retyping the entire line, simply press the
you typed is redisplayed. Use the
the missing “r”. Repeated use of the
characters and then the
key. The statement
key to move the cursor over and insert
key recalls earlier lines. Typing a few
key finds a previous line that begins with those
characters. You can also copy previously executed statements from the
command history window [2].
Interrupting a Command, a Script or a Function
It is often that a user writes a command (or script or a function) that enters
to an endless loop, so it keeps running. Pressing [Ctrl]+[C] once or few times,
it will terminate the execution. Sometimes where the user runs a script that
calls other functions, the interruption with [Ctrl]+[C] might take few seconds
to few minutes to take place.
Current Directory
On the command window toolbar, the user can find the current directory
address bar. Matlab file operations use the current directory and the search
path as reference points. Any file you want to run must either be in the
20
current directory or on the search path (the search path is a default list of
paths that include all folders with Matlab build in functions and toolboxes; to
access this window from the command window go: File>Set Path…). A quick
way to view or change the current directory is by using the current directory
field in the desktop toolbar as shown in Figure 8. To search for, view, open,
and make changes to Matlab - related directories and files, use the Matlab
current directory browser which is called after clicking the icon:
.
Figure[2] 8: Command Window Toolbar with Current Directory
1.5.2 Editor/Debugger
Use the Editor/Debugger to create and debug m-files, which are programs
you write to run Matlab functions [2]. The Editor/Debugger provides a
graphical user interface for basic text editing, as well as for m-file debugging
(Figure 9).
Figure[2] 9: Matlab’s Editor/Debugger
21
It’s like a text editor (e.g. MS Word) suitable for writing executable Matlab
code. Notice that reserved words (e.g. whi l e , i f, e l se , e nd, functi on etc)
appear in blue styling whilst accompanied comments in the programming
code (that can be placed after the comments symbol: “%”) appear in green
letters [2]. Exploit the various menus to become familiar with this window.
For example, by selecting: File>New you can create a new m-file or by
selecting: Debug>Run you can run a saved script that includes various
commands and functions.
1.4.3 Help Options
Matlab is technical software that is enhanced with extensive online help via
various help facilities.
help Command
In first place, if the user knows the topic in which an informative help tip is
needed it can use the he l p command. For instance, if help is needed about
the magic squares, the user types the following expression in the command
window:
“he l p magi c”
and after pressing the [Enter] key, the Matlab response is (Figure 10):
Figure 10: Matlab’s help response on magic squares
22
Type also:
“he l p e l fun”
to view the help results concerning the build-in elementary functions
exhibited in Table 1 (notice also that e l fun is a reserved word).
The problem with the he l p command is that the user must be familiar with
the topic under consideration and the word following the he l p command
must be exact and spelled correctly. For example, the Matlab function that
returns the inverse of a matrix is named as: i nv (type “help inv” to see what
you will get). If the user types “inverse” or “inverce” instead, then Matlab
help will return that such functions cannot be found.
lookfor Command
A more flexible command for perusing help from Matlab, is the l ookfor. If the
user is not familiar with the exact help that is looking, it can use the lookfor,
which looks for the given string in the first comment line of the help text in
all m-files located in Matlab’s toolboxes. For example, type:
“l ookfor inverse”
and Matlab returns all m-files functions that contain in their introductory
comments the word “inverse”. Among them, the user can locate the correct
name for the inverse function (which is simply: i nv) and with the he l p
command can see in detail what this command does. Note that the l ookfor
command is time consuming and sometimes takes up to some minutes to
come up with a result.
The Help Window/Browser
Online help (online here does not refer to any Internet source) can also be
obtained via the Help menu found in the Matlab’s desktop. From the
desktop window select Help>Matlab Help to get the help browser (Figure 11)
with a list of help topics. Through this screen, the user can navigate around
a variety of topics by double clicking on them (this browser displays html
help pages and can be operate like the Internet Explorer).
23
Figure[2] 11: Matlab’s help browser
To become familiar with the Matlab’s accompanied toolboxes, navigate in the
contexts, open up the dropping down choices and get know various topics.
24
Second Section
2. Manipulating Vectors and Matrices
A matrix or an array is the basic element on which Matlab can operate. A 1by-1 matrix forms a scalar or a single number, whereas a matrix with only
one row or column forms a row or column vector respectively. This section
exhibits the mathematical manipulation of vectors (arrays) and of twodimensional matrices.
2.1 Row Vectors
A vector is a list of numbers separated by either space or commas. Each
different number/entry located in the vector is termed as either element or
component. The number of the vector elements/components determines the
l e ngth of the vector. In Matlab, square brackets “[ ]” are used to both define
a vector and a matrix. For instance, the following command returns a row
vector with 5 elements:
Matlab’s command:
>> y=[ 5 exp(2) sign(-5) sqrt(9) pi]
Matlab’s response:
y=
5
7.3891
-1
3
3.1416
Note that the definition of the row vector, the user it free to use any built-in
function as long as this is used properly. In the above definition, e xp is the
exponential, si gn returns the sign, sqrt is the square root and pi represents
p. General speaking and except some special cases, when a function is
applied to a 1-by-1 scalar, the result is a scalar, when applied to a row or
column vector is a row or column vector and when applied to a matrix the
output is again a matrix. This happe ns because Matlab applied the build-in
25
functions element-wise. The l e ngth of the above vector is obtained via the
following command:
Matlab’s command:
>> length(y)
Matlab’s response:
ans =
5
Note that l e ngth is a build-in function that given a vector, it returns its
length. Since the result of this function is not stored in a user-defined
variable, Matlab saves the result in the ans variable. If it is need to save the
vector’s length to a variable named Yl e ngth the command would be:
Matlab’s command:
>> Ylength=length(y)
Matlab’s response:
Ylength =
5
With Matlab, vectors can be easily multiplied by a scalar and added or
subtracted with other vectors of similar length. Moreover, a scalar can be
added or subtracted to or from a vector and smaller vectors can be used to
construct larger ones. All these operations are performed element-wise. Note
that each vector represents a variable. Some examples follow:
Matlab’s command:
>> a=[-1 2 -3]; b=[2 1 2];
>> c=5*a
Matlab’s response:
c=
-5 10 -15
Comments:
An element-by-element multiplication of vector a by 5.
26
Matlab’s command:
>> c1=5+b
Matlab’s response:
c1 =
7
6
7
Comments:
An element-by-element addition of vector b with 5.
Matlab’s command:
>> d=a+b
Matlab’s response:
d=
1
3 -1
Comments:
An element-by-element addition of two equal length vectors.
Matlab’s command:
>> e=[2*a, c, d]
Matlab’s response:
e=
-2
4 -6 -5 10 -15
1
3 -1
Comments:
A larger vector is created after certain manipulations.
To refer to specific elements of the vector, the vector’s name is followed by
the element’s rank in brackets. For instance we can change the values of the
e vector with the following command:
Matlab’s command:
>> e(2)=-99; e(4)=-99; e(6)=-99;
>> e
Matlab’s response:
e=
-2 -99
-6 -99
10 -99
1
3
-1
2.1.1 The Colon Notation
The colon notation “:” can be used to pick out selected rows, columns and
elements of vectors, matrices, and arrays. It is a shortcut that is used to
create row vectors. Moreover, the colon notation is used to view or extract
27
parts of vectors (afterwards, with matrices, the colon can be used to view a
certain part of a matrix). For instance, the following commands produce
three different row vectors:
Matlab’s command:
>> v1=1:8, v2=-4:2:2, v3=[0.1:0.2:0.6]
Matlab’s response:
v1 =
1
2
3
4
v2 =
-4
-2
0
2
5
6
7
8
v3 =
0.1
0.3
0.5
The careful viewer should have notice that the vector creation via the use of
the colon notation has the form: starting_value:step:finishing_value. The
starting_value consists the first value/element of the vector, the
finishing_value is the last value/element of the vector and all other elements
differ by a value equal to step. Also, when the interval between
finishing_value and starting_value is not divisible by the step, the last value
of the vector is not the finishing_value (i.e. in v3 the last element is 0.5 and
not 0.6). The colon notation is also used to view or extract parts of a vector.
See the examples to get an idea.
Matlab’s command:
>> v4=v1(2:4)
Matlab’s response:
V4 =
2
3
4
Comments:
Extracting the 2th, 3rd and 4th elements of v1.
Matlab’s command:
>> v1(2:3:8)
Matlab’s response:
ans =
2
5
8
Comments:
Extracting the 2th, 5th and 8th elements of v1.
28
2.1.2 Column Vectors
Column vectors are created via the use of semi-colon “;” instead of commas
and spaces. Operations with column vectors are similar as with row vectors.
The following examples depict the manipulation of column vectors.
Matlab’s command:
>> cv=[1;4;7;9]
Matlab’s response:
cv =
1
4
7
9
Comments:
Creating a four-element column vector.
Matlab’s command:
>> length(cv)
Matlab’s response:
ans =
4
Comments:
Taking the vector’s length.
Matlab’s command:
>> CV=[cv(1:2)+2; cv(2:3)*5]
Matlab’s response:
CV =
3
6
20
35
Comments:
Creating CV that is a four-element column vector. Its first two
elements are the two first elements of cv increased by 2 whereas
the last two elements are the 2nd and 3rd elements of cv multiplied
by 5.
29
2.1.3 Transporting Vectors
To perform operation with column and row vectors of similar length, it is
first needed to transpose the vectors in order to make them either all row
vectors or column ones. The apostrophe symbol “ ' “ is used to convert a
column vector to a row one and vise versa. Remember that the length of the
vectors must match; otherwise, Matlab will return an error. Experiment with
the following examples to learn the use of transpose command.
Matlab’s command:
>> z1 = [2 -1 3], z2 = z1', z3 = z2'''
Matlab’s response:
z1 =
2
-1
3
z2 =
2
-1
3
z3 =
2 -1
3
Comments:
z1 is a three element row vector. z2 is the transpose of z1. z3 is
similar with z1 since after transposing z2 three times is similar as
transposing once the z2.
Matlab’s command:
>> z1'+z2, z1+z2
Matlab’s response:
ans =
4
-2
6
??? Error using ==> +
Matrix dimensions must agree.
Comments:
z1'+z2 operation involves the addition of two column vectors.
z1+z2 is an illegal operation since a row vector cannot be added
with a column vector.
Note that that Matlab can store empty vectors. This is done as follows:
30
Matlab’s command:
>> Z=[], Z=1:3, Z=[], length(Z)
Matlab’s response:
Z=
[]
Z=
1
2
3
Z=
[]
ans =
0
Comments:
Definition of an empty vector.
Empty vector operation is usually used in cases where the user wants to
turn a non-empty vector to an empty one (to reset all the elements of a
vector).
2.1.4 Vector Manipulations Related to Products, Division, and
Powers
Matlab can perform, scalar products (or inner products) and dot products,
as well as dot division and power operations. The only restriction is that the
length of the vectors must be the same. The priorities concerning vector
manipulations is the same as in the case that we use Matlab as a calculator
(power operations first followed by “*” and “/” followed by “+” and “-“)
2.1.4.1 Scalar Product
The scalar product or otherwise termed as inner product, concerns the
multiplication of two equal length vectors. The symbol “*” is used to carry
out this operation. Given a row vector W and a column vector U of length t:
u1
u
~
~
w = [ w1 , w 2 ,..., wt1 ] , u = 2
M
ut
31
The inner product is defined as the linear combination:
~u
~=
w
t
∑ wi u i
i =1
The following depicts some examples with inner products.
Matlab’s command:
>> w=[1 0 2 -1]; u=[2; 4; -2; 0.5];
>> prod1=w*u, prod2=(2+w)*(u/2), prod3=w*w', prod4=w*u*w*u
Matlab’s response:
prod1 =
-2.5
prod2 =
3.25
prod3 =
6
prod4 =
6.25
Comments:
Producing the inner product of various operations. For example
prod1 is computed as: prod1=(1*2)+(0*4)+(2*(-2))+((-1)*0.5)=-2.5.
2.1.4.2 Dot Product
The dot product involves the multiplication of two similar vectors (to be
either column or row vectors with same length) element-by-element. With
the dot product, a new vector is created. The dot product between the row
~ and ~
vectors w
u T (where the superscript T represents the transpose symbol)
is another row vector with the following form:
~u
~T = [ w u , w u ,..., w u ]
w
1 1
2 2
2 2
32
The dot product in Matlab is performed via the “.*” symbol. By the use of dot
product we can get the inner product. This is explained in the following
examples:
Matlab’s command:
>> dprod1=w.*u', dprod2=u'.*u'.* w
Matlab’s response:
dprod1 =
2
0
-4
-0.5
dprod2 =
4
0
8
-0.25
Comments:
Producing the dot product of various operations. For example
dprod1 is computed as: dprod1=[1*2, 0*4, 2*(-2), (-1)*0.5].
Matlab’s command:
>> inner1=sum(w.*u'), inner2=sum((2+w).*(u'/2))
Matlab’s response:
inner1 =
-2.5
inner2 =
3.25
Comments:
Producing the summation of dot product of various operations.
When the sum function is used with a dot product, the result is
the inner product of that operation.
In vector manipulations, dot product is performed after dot power (see the
following section).
2.1.4.3 Dot Division and Power
The dot division does not exist mathematically, but for programming
purposes, Matlab includes such operation. The dot division can be used to
divide a vector with another vector of similar characteristics and also to
divide a vector with a scalar. Through the following examples the use of dot
division is outlined. Pay attention on the cases where a dot division
produces pathological results.
33
Matlab’s command:
>> d_div1=-3:1.5:3, d_div2=1:5
>> d_div2./d_div2, d_div1./d_div2, d_div2./5
Matlab’s response:
d_div1 =
-3.0000 -1.5000
d_div2 =
1
2
3
4
5
ans =
1
1
1
1
1
ans =
-3.0000 -0.7500
ans =
0.2000
0.4000
0
1.5000
3.0000
0
0.3750
0.6000
0.6000
0.8000
1.0000
Comments:
Examples of dot division.
Matlab’s command:
>>d_div2./d_div1
>> d_div2(3)=0; d_div1./d_div2
>> 1/d_div1
Matlab’s response:
Warning: Divide by zero.
(Type "warning off MATLAB:divideByZero" to suppress this
warning.)
ans =
-0.3333 -1.3333
Inf
2.6667
1.6667
Warning: Divide by zero.
(Type "warning off MATLAB:divideByZero" to suppress this
warning.)
ans =
-3.0000 -0.7500
NaN
0.3750
0.6000
??? Error using ==> /
Matrix dimensions must agree.
Comments:
Examples of pathological results of dot division. In the first case,
Matlab returns the result after displaying a warning concerning
the division of a number with zero that leads to an infinity
quantity. Observe that Matlab returns an Inf for such operations.
Likewise, in the second case, the division of 0/0 is not defined
and a Not-a-Number, NaN, is returned in the vector. In the third
34
and a Not-a-Number, NaN, is returned in the vector. In the third
case, the inverse of each vector element is required, but Matlab
returns an error since for such operation the “./” and not “/”
should have been used instead.
Example: Examine the following limit:
lim
e x − e −x
x →∞ e x
+ e −x
Matlab’s command:
>>x=[0.5 1 5 25 50 100 300];
>>(exp(x)-exp(-x))./(exp(x)+exp( -x))
Matlab’s response:
ans =
0.4621 0.7616 0.9999 1.0000 1.0000
Comments:
Apparently, the limit converges to unity.
1.0000
1.0000
The dot power of vectors works in a similar way as with other dot products.
Usually there is the need to square (or to rise to some other power) the
elements of a vector. This can be done with the dot power operation as
explained in the following example set.
Matlab’s command:
>> d_power=sqrt(0:log(3):6)
>> d_power.^2, d_power.^4, d_power.* d_power, ans.*ans
Matlab’s response:
d_power =
0 1.0481
1.4823
1.8154
2.0963
2.3437
3.2958
4.3944
5.4931
ans =
0
1.0986
2.1972
0
1.2069
4.8278 10.8625 19.3112 30.1737
0
1.0986
2.1972
0
1.2069
4.8278 10.8625 19.3112 30.1737
ans =
ans =
3.2958
4.3944
5.4931
ans =
35
Comments:
Examples of dot power. The second or the forth power of a certain
vector can be defined either with the dot power or the dot product
operation.
Before leaving this section, the reader should note that dot power of vectors
is performed before any other operation, followed by the dot product and the
dot
division.
Off
course,
if
a
complex
vector
command
involves
manipulations into brackets, these are executed before any other action.
2.1.4.3 Some Useful Vector Functions
Table 2 lists some useful function that can be used with row and column
vectors. This list is by no way exhaustive.
Basic Information
Elementary Matrices and Arrays
Generate linearly spaced
di sp
Display array
l i nspace
vectors
Generate logarithmically
di spl ay Display array
l ogspace
spaced vectors
i se mpty True for empty vector
one s
Create array of all ones
True if arrays are
Uniformly distributed
i se qual
r a nd
identical
random numbers and arrays
l e ngth Length of vector
ze ros
Create array of all zeros
Operations and Manipulation
cumprod Cumulative product
me an
Average of array
cumsum Cumulative sum
me di an Median of array
e nd
Last index
mi n
Minimum elements of array
Find indices of
Sort elements in ascending
f i nd
sort
nonzero elements
order
Maximum elements
max
sum
Sum of array elements
of array
Table 2: Various functions that can be used with vectors.
Use the he l p facilities to see how these functions can be used. The following
illustrate the use of some of these functions.
Matlab’s command:
>> clear; clc;
>> x=[ ]; isempty(x)
>> x=linspace(1, 10, 6), x=logspace(0.1, 0.5, 6); x(7)=0.1; x
>> sort(x), cumsum(x), [Max, I]=max(x), x(end)
36
Matlab’s response:
ans =
1
x=
1.0000
2.8000
4.6000
6.4000
8.2000 10.0000
x=
1.2589
1.5136
1.8197
2.1878
2.6303
3.1623
0.1000
ans =
0.1000
1.2589
1.5136
1.8197
2.1878
2.6303
3.1623
ans =
1.2589
2.7725
4.5922
6.7799
9.4102 12.5725 12.6725
Max =
3.1623
I=
6
ans =
0.1000
Comments:
Examples with vector functions. The first command instructs for
the creation of an empty vector. The i se mpty function returns 1
for the true statement of an empty vector. Afterwards, l i nspace is
used to generate a row vector of 6 linearly equally spaced points
between 1 and 10 whereas l ogspace is used to generate a row
vector of 6 logarithmically equally spaced points between decades
10^0.1 and 10^0.5. “x(7)=0.1” instructs for the creation of a
seventh element for the x vector. “ sort(x)” sorts the elements of x
in ascending order, “cumsum(x)” is a vector containing the
cumulative sum of the elements of x, “[Max, I]=max(x)” returns in
Max the maximum value of the vector x and in I the index of the
maximum element. The last command, “x( e nd)” returns the last
element of the x vector.
2.2 Two Dimensional Arrays (Matrices)
A m × n matrix is a rectangular array that has m rows and n columns. For
example, a 2-by-4 matrix can be the following one:
a 12
a
A 2 × 4 = 11
a 21 a 22
a 13 a 14
a 23 a 24
37
It is obvious that the above matrix can be decomposed to either 2 row
vectors of 1 × 4 dimensions or to 4 column vectors of 2X 1 . So, row and
column vectors are special cases of a two dimensional array (matrix).
If we let, a 11 = 1 , a 21 = −2 , a 12 = −2 , a 22 = 2 , a 13 = 5 , a 23 = 4 ,
a 12 = −3 and a 24 = 1 , then the “A” matrix is reformed to:
1
A 2× 4 =
− 2
−2 5
2 4
− 3
1
The subscripts in each element of the matrix denote the element’s position.
For instance, the position of a 23 is 2nd row, 3rd column. Matlab stores
matrices using this rational. Having in mind that a two dimensional array is
a composition of row vectors, we can use spaces (or commas) to define its
row vectors and semicolons to separate them. The above matrix can be
easily created as follows:
Matlab’s command:
>> A=[ 1 -2 5 -3; -2 2 4 1]
Matlab’s response:
A=
1 -2
5 -3
-2
2
4
1
Comments:
Creation of a 2-by-4 matrix.
To show that row and column vectors are special cases or a two dimensional
array (matrix) elaborate on the following exampl es:
Matlab’s command:
>> B=linspace(1, 4, 5); C=1:5; D=[-4:-1, NaN, Inf 1];
>> A1=[B; C], A2=[A1; A1], A3=[B -9 -5;D]
Matlab’s response:
A1 =
1.0000
1.0000
1.7500
2.0000
2.5000
3.0000
3.2500
4.0000
4.0000
5.0000
38
A2 =
1.0000
1.0000
1.0000
1.0000
1.7500
2.0000
1.7500
2.0000
2.5000
3.0000
2.5000
3.0000
3.2500
4.0000
3.2500
4.0000
4.0000
5.0000
4.0000
5.0000
A3 =
1.0000 1.7500 2.5000 3.2500 4.0000 -9.0000 -5.0000
-4.0000 -3.0000 -2.0000 -1.0000
NaN
Inf 1.0000
Comments:
Various manipulations with matrices.
The examples above, illustrate the case where a larger matrix can be created
from smaller ones. Also, pay attention that Matlab returns an error if the
user tries to combine row or column vectors with different lengths to create
a two dimensional array.
Usually, it is imperative need to store the size of a matrix in some variables.
This can be done via a build in function named as si ze :
Matlab’s command:
>> [m1 n1]=size(A1); [m2 n2]=size(A2); [m3 n3]=size(A3);
>> M_N=[m1 n1; m2 n2; m3 n3]
Matlab’s response:
M_N =
2
5
4
5
2
7
Comments:
Using the si ze function to find the size of various matrices. Each
row of the M_ N matrix contains the size of matrices A1, A2 and
A3 respectively.
2.2.1 Transpose of a Matrix
Recall matrix “A” that was defined earlier. The transpose of “A”, symbolized
in linear algebra as “AT” is the following:
a 12
a
A 2 × 4 = 11
a 21 a 22
a 13 a 14
,
a 23 a 24
a 11 a 21
a
T
12 a 22
A 4× 2 =
a 13 a 23
a 14 a 24
39
It is the same idea with the transpose of a row vector to a column one and
vise versa. The transpose of an m × n matrix is an n × m one that is found if
the rows of the original matrix become columns in the transposed one.
Recall that the transpose in Matlab is performed with “ ' ”. See the following
examples to digest this issue.
Matlab’s command:
>> A4=[1 2 3; 4 5 6], size(A4), A4', size(A4'), A5=[A4' A4']
Matlab’s response:
A4 =
1
4
2
5
ans =
2
3
ans =
1
2
3
4
5
6
ans =
3
2
3
6
A5 =
1
4
1
4
2
5
2
5
3
6
3
6
Comments:
Exploiting the transpose of a matrix.
2.2.2 Elaborating on Parts of Matrices – The Colon Notation
As noted before, in Matlab, a matrix element position is indexed according to
the row and column number. Recall the aforementioned “A” matrix:
1
A 2× 4 =
− 2
−2 5
2 4
− 3
1
If someone wants to extract the elements: a 12 , a 23 , , and a 24 , this can be
done in the following way ( A has already been created and should be stored
40
in the workspace; use the who function to view the variables that you have
saved in the workspace or view them from the workspace browser):
Matlab’s command:
>> A(1,2), A(2,3), A(2,4)
Matlab’s response:
ans =
-2
ans =
4
ans =
1
Comments:
Extracting specific elements from a matrix.
So, in Matlab, to refer to a certain matrix element, after the matrix name the
element’s index/position is enclosed in parenthesis. This is similar with the
indexing of vectors elements with the exception that in the case of matrices,
two indexes should be used (the first one indicates the row number whilst
the second the column number). In general, the syntax for manipulating a
matrix element in Matlab is:
“K(row_index, column_index)”
where K is an m × n matrix, row_index indicates the row in which an
element lays and column_index the according column. The upper left
position in a matrix has (1,1) coordinates. row_index can take all integer
values smaller than m, inclusive, while column_index can also take all
integer values smaller than n, inclusive (note that Matlab can handle
multidimensional arrays just by putting additional indexes to control the
higher dimensions).
Moreover, Matlab has an additional way to refer to matrix elements just by
using a single index number in the brackets after the declaration of the
matrix name. Starting from the upper left element that represents the first
element (1)of the matrix, further reference to additional elements is done
incrementally one by one and column-wise. That is, the element with
41
position (2,1) is taken to be the second (2), the (3,1) the third and finally the
(m, n) element is the last one (n*m). View the following example to
understand this king of matrix indexing.
Matlab’s command:
>> H=magic(4), H(1), H(2), H(9), H(16)
Matlab’s response:
H=
16
5
9
4
2
11
7
14
3 13
10
8
6 12
15
1
ans =
16
ans =
5
ans =
3
ans =
1
Comments:
Extracting specific elements from a matrix using single indexing.
For matrices, the colon notation “:” plays an important role. Colon can be
used to extract either a specific part of a matrix, or to view a whole row, a
whole column or a sub-matrix extracted from the original one. Earlier, the
colon was used to define vectors and it has been explained that it creates
elements from a starting_value through a finishing_value equally spaced
according to a defined step (if the step is not defined, then the step is taken
to be 1). In Matlab, a certain row of a matrix can be extracted by placing the
colon in the row_index, “K(:,column_index)”, and a certain column by placing
the colon in the column_index, “K(row_index:,:)”. A sub-matrix that is
composed by the r1 to r2 rows (r1=r2) and c1 to c2 columns (c1=c2) of the
original matrix can be retrieved according to the following syntax:
“K(r1:r2, c1:c2)”
42
In addition, there are special cases where the step is defined to be a different
integer number other than 1. Some paradigms follow:
Matlab’s command:
>> A(:,1), A(1,:), A(:,1:3), A=[A', A'.*2], A(2:3,3:4)
>> A(1:3,1:2)=A(2:end,3:end)
Matlab’s response:
ans =
1
-2
ans =
1 -2
5
ans =
1 -2
-2
2
5
4
-3
A=
1
-2
5
-3
ans =
-4
10
-2
2
4
1
2
-4
10
-6
-4
4
8
2
4
8
ans =
-2 -4
A=
-4
4
2 -4
10
8 -4
4
-6
2 10
8
-3
1 -6
2
Comments:
The first command, instructs for the extraction of the first column
whilst the second for the extraction of the first row. The following
one instructs for the extraction of the 1st, 2nd and 3rd columns.
Afterwards, A is re-built; the following command instructs for the
extraction of the sub-matrix that is composed from the elements
of A that are included in: 2nd and 3rd row – 3rd and 4th columns.
The following command is a special case where the step in the
colon expression is different than 1. The last command is a more
tricky use of the colon.
43
2.2.2 Matrix Basic Manipulations
Subtraction and multiplication with a scalar are similar as with the vector
case. Matrix dimensions ( si ze ) must match when performing manipulations
with addition and subtraction. Some examples follow:
Matlab’s command:
>> J=[-1 2 3 1; 5 2 4 2; 1 1 2 0]; I=[1 4 5 2; 8 7 5 1; -1 1 -1 1];
>> J+2*I, J(:,1)+I(:,2), J(1,:)-1/4*I(2,:)
Matlab’s response:
ans =
1
21
-1
10
16
3
13
14
0
5
4
2
ans =
3
12
2
ans =
-3.0000 0.2500 1.7500 0.7500
Comments:
Basic matrix addition, subtraction and scalar multiplication.
2.1.4 Matrix Manipulations Related to Products, Division, and
Powers
Similar rules as with the case of vectors apply to matrix manipulations
related with dot ope rations and products of matrices.
2.1.4.1 Matrix Dot Product, Division and Powers
It is straightforward to generalize the properties of dot operations from the
case of vectors to the case of two-dimensional arrays. The operations are
again performed element-by-element. Work on the following examples to
learn the use of dot operations with matrices (remember which operations
come first).
44
Matlab’s command:
>> clear; U=[-1 2 1; 0 -2 3]; V=[1:3; 5 2 4];
>> U.^2, U.*V, (1./V).^2.*U, U.^U
Matlab’s response:
ans =
1
0
4
4
1
9
ans =
-1
4
0 -4
3
12
ans =
-1.0000 0.5000
0
-0.5000
ans =
-1.0000 4.0000
1.0000 0.2500
Comments:
Dot operations with
0.1111
0.1875
1.0000
27.0000
two-dimensional arrays.
2.1.4.2 Matrix to Vector Product – Matrix to Matrix Product
A matrix can be multiplied with a vector or a matrix as long as the following
rule concerning their dimensionality/sizes holds:
(m × n ) × (n ×l )
That is, the first’s matrix columns equal the second’s rows. A matrix “A”
with dimensions m × n can be multiplied with a matrix “B” with dimensions
m × l resulting to a matrix “C” with dimensions m × l :
Cm×l = Am×n × B m×l
The above matrix “A” can be multiplied with a 1 × m row vector “R1” from
left to produce a 1 × n row vector “R” while “A” can be multiplied with an
n × 1 column vector “C1” to the right to produce a column vector “C” with
m × 1 dimensions:
R1×n = R 11×m × Am×n
45
Cm×1 = Am×n × C 1n ×1
Let’s define the “A” and “B” matrices:
a 12
a
A 2 × 4 = 11
a 21 a 22
a 13 a 14
,
a 23 a 24
b11
b
B 4 × 2 = 21
b31
b41
b12
b 22
b 32
b 42
Like linear algebra, Matlab products with matrices (and/or vectors) are
calculated as follows:
c
c
C 2×2 = A2×4 × B 4×2 = 11 12 ⇒
c 21 c 22
a b + a 12b 21 + a 13b 31 + a 14b41 a 11b12 + a 12b 22 + a 13b32 + a 14b42
C 2 × 2 = 11 11
a 21b11 + a 22b 21 + a 23b31 + a 24b41 a 21b12 + a 22b 22 + a 23b 32 + a 24b 42
That is, the element in the (1,1) position of the new matrix “C” if the inner
product of the 1st row of “A” with the 1st column of “B”, the (1,2) element of
“C” is the inner product of the 1st row of “A” with the 2nd column of “B” and
so on. Work through the following examples to digest this topic.
Matlab’s command:
>> clear; A=[ 1 -2 5 -3; -2 2 4 1]; B=[2 3;1 0;2 -1;1 4]; A_B=[A;B'];
>> R1=[-2 -1 3 2]; C1=[1; -1; 2; 0];
>> C=A*B, Row=R1*A_B, Col= A_B*C1, A*(A_B*A_B)*B
Matlab’s response:
C=
7 -14
7 -6
Row =
12
5 -10
16
46
Col =
13
4
5
1
ans =
39 -310
297 314
Comments:
Matrix-vector and matrix-matrix products.
2.1.5 Special Cases of Matrices
Matlab has some very useful build-in matrices functions that ease the
manipulation of two dimensional arrays. These functions usually take as
input (at least) the matrix dimension and return a certain result. Table 3
exhibits these very useful functions accompanied with a short explanation of
their use.
In the case where m is equal to n this returns an identity
matrix
one s(m,n) Creates an m-by-n matrix of ones
When V is a m-by-m matrix returns the elements of the main
di ag(V)
diagonal.
rand(m,n) Creates an m-by-n matrix with random entries
ze ros(m,n) Creates an m-by-n matrix of zeros
Table 3: Various functions that can be used with vectors.
e ye (m,n)
Examples with the above matrix-functions follow:
Matlab’s command:
>> eye(3,2), ones(2,3), diag([2 3; 1 -2]), rand(2,2), zeros(1,2)
Matlab’s response:
ans =
1
0
0
0
1
0
ans =
1
1
1
1
1
1
ans =
2
-2
47
ans =
0.9501
0.2311
0.6068
0.4860
ans =
0
0
Comments:
Examples with matrices build-in functions.
2.1.5 Additional Useful Matrix Functions
Functions that are exhibited in Table 1 can also been applied to a two
dimensional arrays because vectors are special cases of matrices (and vise
versa). Additional build-in functions are illustrated in Table 4.
Basic Information
Elementary Matrices and Arrays
ndi ms Number of dimensions
bl kdi ag Block diagonal concatenation
numel Number of elements
Operations and Manipulation
de t
Determinant
r a nk
Matrix rank
e xpm Matrix exponential
sortrows Sort rows in ascending order
fl i pl r Flip matrices left-right
sqrtm
Matrix square root
fl i pud Flip matrices up-down
t r a ce
Sum of diagonal elements
i nv
Matrix inverse
tr i l
Lower triangular part of
matrix
l ogm Matrix logarithm
tr i u
Upper triangular part of
matrix
norm Matrix or vector norm
Table 4: Various functions that can be used with vectors.
Moreover, type: “he l p matfun” to view some very useful matrix functions
related with numerical linear algebra.
2.1.6 Example: System of Linear Equations
Many times, a researcher has to solve a system of linear equation
simultaneously. In matrix notation, such problem is formulated as:
Ax = b
where “A” is a coefficient matrix, “x: is the set (column) of unknowns and “b”
is a column vector. In an equation-wise format, the above is equal to:
48
a 11 x 1 + a 12 x 2 + ... + a 1m x m = b1
a 21x 1 + a 22 x 2 + ... + a 21m x m = b2
M
a n 1 x 1 + a n 2 x 2 + ... + a nm xm = bn
The solution of the above system can be expressed as:
x = A −1b
given that “ A −1 ” (that represents the inverse matrix of “ A ”) exists and the
number of equation, n, is equal or greater than the number of unknowns, m.
A unique solution to the above equation system exists when: n=m.
Matlab has standard and efficient specialized routines to solve such systems
like the ml di vi de function (called alternatively with “\”). Otherwise, a quick
way (but some times non practical and inaccurate if the number of
equations is extremely large) to solve the above system is via the inverse
function, i nv (note that the i nv can be used only with square matrices). View
the following example to understand how you can solve a small system of
linear equations:
Matlab’s command:
>> clear; A=[2 4 3; -2 -4 2; 6 4 2]; b=[2 ;4;1];
>> x1=inv(A)*b, x2=A\b
Matlab’s response:
x1 =
0.0500
-0.4250
1.2000
x2 =
0.0500
-0.4250
1.2000
Comments:
Two ways for solving a system of linear equations.
49
To see that these two procedures lead to different results, elaborate on the
following example (search online help to see the use of the command:
pascal ):
Matlab’s command:
>> clear; A=pascal(10); b=[5; -2; 4; 8; 1; 2; 0; -6; 2; 3];
>> x1=inv(A)*b;, x2=A\b;
>>diff=x1-x2
Matlab’s response:
diff =
-1.0328 e-006
9.0204 e-006
-3.4539 e-005
7.6293 e-005
-0.00010781
0.0001013
-6.3407 e-005
2.5521 e-005
-5.9979 e-006
6.2738 e-007
Comments:
For even moderate linear systems, the two methods ( i nv and “\”)
lead to different solutions. If high precision is required, then the
researcher should prefer the “\”.
The most proper way for large systems is the use of “\”. See the help
facilities for details on i nv and on “\”.
50
Third Section
3. Plots and Graphs (2D and 3D)
It is quite easy to create a plot or a graph by using the variables or
parameters that have already been stored in the Matlab’s workspace. Matlab
offers a variety of build-in functions for creating simple two dimensional
plots, 3 dimensional surface plots, to combine plots to a larger one and so
on. The following subsections are a very brief and an elementary reference to
the visualization capabilities of Matlab.
3.1 Creating 2D Line Plots
The basic function for the creation of a simple 2D line plot is called: plot. Let
be a row or column vector with real data named Y, with elements “y1, y 2, …,
yn”. If pl ot is called as: “ pl ot(Y)”, then a linear plot of the elements of Y versus
its index will appear (the pl ot function creates/plots the pairs: (1, y 1), (2, y2),
…, (n, yn) and connects them with a line). If for each “yi” we have an
accompanied “xj” coordinate, then the function “ pl ot(X,Y)” plots all pairs: (x1,
y1), (x2, y2), …, (xn, yn) and connects them with a line. Note that vectors Y
and X must share the same length. Additionally, if the data to be plotted are
stored in a two dimensional array, then the arguments for the pl ot function
can be done via the use of colon notation “:”. It is very easy to plot the
following function in the range [0,5]:
y=
2 x 2 + 5x − 1
x3 −5
Matlab’s command:
>> clear; x=0:0.5:5; y=(2*x.^2+5*x-1)./(x.^3-5); plot(x,y);
>> x=0:0.2:5; ; y=(2*x.^2+5*x-1)./(x.^3-5); plot(x,y);
51
Matlab’s response:
6
4
2
0
-2
-4
-6
-8
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
20
15
10
5
0
-5
-10
-15
0
Comments:
Plot of a function. The use of dot operations is prominent for this
task. Note that the plot’s smoothness is controlled by the density
of the x vector. In the second plot where the x is denser, the
function plot is smoother.
3.1.1 Plot Edit Mode
If you have already type the aforementioned commands on the Matlab
command window, you will have noticed that the plots that you see, appear
in a figure window (i.e Figure 10) that offers a variety of tools that allow you
to edit and customize the plot under consideration by using a point and
click style editing mode.
52
Figure[2] 10: The figure window
This figure window has tools that look like a photo editor (e.g. Microsoft®
Photo Editor). You can select objects in a graph, cut, copy, paste, move and
resize objects, zoom in and zoom out at certain areas of the plot, change the
settings of the axes, print or save the figure for a later use or even to export
the plot in a certain format (e.g. *.emf, *.bmp, *,ipg, *.tif, etc). Create a figure
and play around with the various tools to learn their use.
The plots that are included in this handout (except the ones that were
copied from [2]) have been exported from the figure window in an enhanced
metafile format (*.emf). To export a plot, from the figure window go:
File>Export, and from the window that appears choose the exporting format,
give a name to the file and save it in a folder of your choice. By doing this,
you can easily insert plots from Matlab to a text editor like Microsoft® Word.
3.1.2 Functions and Style Facilities Related to Plots
The blue solid line is the default style for the plots. This of course can
change. Matlab gives the user the option to define a different line color and
53
to mark each plotted point with a symbol. To do this, the user should call
the plot function as:
“pl ot(X,Y, '? ??')”
where “?” represents the color, “?” the mark style and “?” the line style (if
not given, then Matlab uses a default style).
Table 5 tabulates the plot
facilities (see also the online help).
Symbol
g
r
c
m
y
k
Color (?)
Green
Red
Cyan
Magenta
Yellow
Black
Symbol
-, :, -., --
Symbol
., o, x
+, *, s
d, v
^, <, >
p, h,
Table 5: Plot colour and line styles.
Line Style (? )
Solid, dotted, dash dot and dashed
Mark Style (?)
Point, circle and x-mark
Plus, star and square
Diamond and triangle down
Triangles: up, left and right
Pentagram, hexagram and solid
Moreover, Table 6 lists additional commands that are useful when using the
pl ot function.
Function
axi s
cl f
cl ose (all)
fi gure
gri d on/off
gte xt('text')
hol d on/off
Comment
Sets the minimum and maximum values of axes.
Clear the current figure.
Closes the current (all) figure(s).
Creates a new figure window.
Adds/removes major grid lines to the current axes.
Adds text to a figure manually, by the use of mouse.
hol d on/off holds the current plot and all axis
properties so that subsequent graphing commands
add to the existing graph.
l e ge nd('text')/l e ge nd off Adds (removes) a legend to the graph.
l ogl og
The same as with pl ot but logarithmic scale axes
are used.
se mi l ogx
The same as with pl ot with the exception that
logarithmic scale is used for X-axis.
se mi l ogy
The same as with pl ot with the exception that
logarithmic scale is used for Y-axis.
subpl ot
Breaks the current figure to subplots.
ti tl e ('text')
Adds a title above the figure.
xl abe l ('text')
X-axis label
yl abe l ('text')
Y-axis label
Table 6: Various functions that help in the creation of 2D-plots.
54
View the following examples to digest the plot facilities.
Matlab’s command:
>> plot(x, y, 'md: '); figure; plot(x, y, 'r*--'); hold on;
>> y1=rand(1,length(y)), plot(x,y1, 'bo'); plot(x,y1, 'r+');
>> xlabel('X-values'); ylabel('Y-values'); title('This is a plot');
>> close all; plot(x,y, 'bp--', x, log(y1.^2), 'rh', x, log(y1.^2),'bs');
Matlab’s response:
20
15
10
5
0
-5
-10
-15
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
3
3.5
4
4.5
5
This is a plot
20
15
10
5
Y-values
0
-5
-10
-15
0
0.5
1
1.5
2
2.5
X-values
55
20
15
10
5
0
-5
-10
-15
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
Comments:
Experimenting with various functions and facilities related with
the plots. The last pl ot command shows how few plots can be
depicted in one figure without using the hol d on command.
The following examples, concern the creation of some subplots in one figure
window. If you view the online help for the subpl ot command, you will see
that it takes three input arguments. That is, it is called as:
“subpl ot(m,n,p)”
It breaks the figure window into an m-by-n matrix of small axes, selects the
p-th axes for the current plot, and returns the axis handle. The axes are
counted along the top row of the figure window, then the second row, etc.
The subpl ot function instructs which subplot is handled at the current time.
After the subpl ot command, a pl ot command should follow. See the following
examples:
Matlab’s command:
>> close all; subplot(2,3,1); plot(x,y, 'r--'); title('Subplot 1');
>> subplot(2,3,2); plot(x,y1, 'y*'); title('Subplot 2');
>> subplot(2,3,3);
>> subplot(2,3,5); plot(randn(1,30), 'bo:'); title('Subplot 5');
>> subplot(2,3,6); plot(x,y, 'bp--', x, (y1.^2), 'rh', x, log(y1.^2),'bs');
>> title('Subplot 6');
56
Matlab’s response:
Subplot 1
Subplot 2
20
10
1
1
0.8
0.8
0.6
0.6
0.4
0.4
0.2
0.2
0
-10
-20
0
2
4
6
0
0
2
4
6
0
0
Subplot 5
20
1
10
0
0
-1
-10
0
10
20
1
Subplot 6
2
-2
0.5
30
-20
0
2
4
6
Comments:
Experimenting with the subpl ot command. The first two input
arguments to the subpl ot function define the dimensionality of the
figure window. If m is the first input arguments and n the second,
then the figure window breaks to an m-by-n plot matrix. The third
input to the subpl ot function designates the current subplot to be
handled. Starting from the upper left corner and moving row-wise to
the lower right corner, 1 refers to the first subplot, 2 to the second
and mn to the last one. After each subpl ot command, the pl ot
command should follow. In the current examples, the commands
instruct for the creation of a 2-by-3 subplot matrix. The 1st, 2nd, 5th
and 6th subplots are used whilst the 3rd and 4th are currently unused.
Note that if the subpl ot command is avoided for any subplot, then its
space on the figure window stays empty. If only the subpl ot is called
as with the case of the third subfigure, then a blank figure appears in
the figure window.
Moreover, Matlab offers a variety of options to customize the graph. For
example, a more general calling syntax for the pl ot is:
“pl ot(X, Y, '? ??', 'PropertyName', PropertyValue, ...)”
57
where “PropertyName” relates with an element of the plot and
“PropertyValue” is defined by the user. Some useful properties concern the
following:
•
“LineWidth” - specifies the width (in points) of the line.
•
“MarkerEdgeColor” - specifies the color of the marker or the edge color
for filled markers (circle, square, diamond, pentagram, hexagram, and
the four triangles).
•
“MarkerFaceColor” - specifies the color of the face of filled markers.
•
“MarkerSize” - specifies the size of the marker in units of points.
View the following examples to conceptualize this issue:
Matlab’s command:
>> plot(x,y,'bd-.', 'LineWidth', 2, 'MarkerSize', 11, ...
'MarkerFaceColor', 'r', 'MarkerEdgeColor', 'g')
Matlab’s response:
20
15
10
5
0
-5
-10
-15
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
Comments:
An example of a plot that uses some of the pl ot properties.
Besides these 2D visualization facilities, Matlab can be used to create bar
charts, pie charts, histograms, stems plot, stairstep plots, errorbars etc. Use
the online help and the help browser to see how you can use these
visualizations facilities and learn more about the pl ot properties.
58
3.2 Creating 3D Graphs
Matlab offers fancy 3-dimensional line plots and surface graphs.
3.2.1 Creation of 3D Line Plots
There is the function: pl ot3 which its use is similar as with the function: plot,
with the difference that an additional input argument corresponding to the
additional dimension is required (the additional dimension is symbolized as
“z”). pl ot3 is used to plot lines or point coordinates in the 3D space. Let use
the pl ot3 to create a 3D helix:
Matlab’s command:
>> clear; g=linspace(-5*pi,5*pi,200); plot3(sin(g),cos(g),g,'r*-');
>> xlabel('x'); ylabel('y'); zlabel('z'); title('A helix');
Matlab’s response:
A helix
20
15
10
5
0
z
-5
-10
-15
-20
1
1
0.5
0.5
0
0
-0.5
y
-0.5
-1
-1
x
Comments:
Creating a helix with the pl ot3 function.
3.2.2 Creation of 3D Mesh and Surface Graphs
There are also many commands that lead to the creation of 3D surfaces.
Recall that to create a surface of two variables, at each pair of (x,y) a
59
functional expression, z=f(x,y), is evaluated. Usually, we evaluate the z
behavior in a certain area of the (x,y)-plane in which z has some interesting
properties (e.g. it presents a minimum, a maximum or a saddle point).
Suppose that a x vector that defines the x-axis (abscissa) and a y vector that
defines the y-axis (ordinate) exist and define the (x,y)-plane on which we
would like to create the 3D surface of z=f(x,y). To plot the surface, it is
needed to create a grid of sample points (most preferable with high density
and this is defined by the difference between the elements of x and y) that
covers the rectangular domain of the (x,y) plane in order to generate X and Y
matrices consisting of repeated rows and columns of x and y, respectively,
over the domain of the function. Then these matrices will be used to
evaluate and graph the function.
The me shgri d function transforms the domain specified by two vectors, x
and y, into matrices, X and Y. You then use these matrices to evaluate the
z=f(x,y). The rows of X are copies of the vector x and the columns of Y are
copies of the vector y.
We will see how we can plot a 3D surface via an example. Let say that we
need a graph of the well know peaks function that has the following
functional form:
2
2
2
2
2
2
x
1
Z = f ( x , y ) = 3( 1 − x ) 2 e − x −( y +1) − 10( − x 3 − y 5 ) e − x −y − e −( x +1) −y
5
3
We want to examine this function in the rectangular space of (x,y)-plane
defined as:
−2≤x ≤2
− 4 ≤y ≤ 4
Since Matlab understands combinations of (x,y,z) pairs only, it is needed to
evaluate Z at various points (the number of these points defines the surface
smoothness) that lay in the above rectangular space. me shgri d can be used
to create the desired grid of points. The following code lead to the generation
of the grid:
60
Matlab’s command:
>> clear; x=-2:1:2; y=-4:1:4; [X,Y]=meshgrid(x,y)
>> plot(X,Y, 'rh'); axis([-3 3 -5 5]); xlabel('x-axis'); ylabel('y-axis');
>> title('Meshgrid');
Matlab’s response:
X=
-2
-2
-2
-2
-2
-2
-2
-2
-2
-1
-1
-1
-1
-1
-1
-1
-1
-1
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
2
2
2
2
2
2
2
2
2
Y=
-4
-3
-2
-1
0
1
2
3
4
-4
-3
-2
-1
0
1
2
3
4
-4
-3
-2
-1
0
1
2
3
4
-4
-3
-2
-1
0
1
2
3
4
-4
-3
-2
-1
0
1
2
3
4
Meshgrid
5
4
3
2
1
0
y-axis
-1
-2
-3
-4
-5
-3
-2
-1
0
x-axis
1
2
3
Comments:
Creating the grid necessary for plotting a 3D surface. me shgri d
takes as inputs the vectors x and y that define the (x,y)-plane that
should be used to evaluate Z and returns two matrices ( X and Y)
that if taken together, generate various (x,y) pairs that lay in the
rectangular domain. The subsequent 2D plot of X and Y shows
61
rectangular domain. The subsequent 2D plot of X and Y shows
how the grid is sampled.
Now, we should evaluate the Z at each pair of the grid and generate the
surface plot. This is done with the following code:
Matlab’s command:
>> Z =3*(1-X).^2.*exp( -(X.^2) - (Y+1).^2)- ...
10*(X/5-X.^3-Y.^5).*exp( -X.^2-Y.^2)-1/3*exp( -(X+1).^2-Y.^2);
>> figure(1); mesh(X,Y,Z); xlabel('x'); ylabel('y'); zlabel('Z');
>> figure(2); surf(X,Y,Z); xlabel('x'); ylabel('y'); zlabel('Z');
Matlab’s response:
6
4
2
0
Z
-2
-4
-6
4
2
2
1
0
0
-2
y
-4
-1.5
-1
1.5
0.5
-0.5
-2
x
62
6
4
2
0
z
-2
-4
-6
4
2
0
0
-2
y
-4
-2
-1.5
-1
0.5
1
1.5
2
-0.5
x
Comments:
Creating the 3D mesh and a 3D surface. The function is not smooth
because the dense of the x and y was too low.
With the above code, a 3D mesh and a 3D surface is created. It is apparent
that the surfaces are not smooth because the original density of x and y
vectors was too low. In the following, we re-create the mesh and surface with
higher densities.
Matlab’s command:
>> x=-2:0.25:2; y=-4:0.5:4; [X,Y]=meshgrid(x,y);
>> Z =3*(1-X).^2.*exp( -(X.^2) - (Y+1).^2)- ...
10*(X/5-X.^3-Y.^5).*exp( -X.^2-Y.^2)-1/3*exp( -(X+1).^2-Y.^2);
>> figure(1); mesh(X,Y,Z); xlabel('x'); ylabel('y'); zlabel('Z'); title('Peaks')
>> figure(2); surf(X,Y,Z); xlabel('x'); ylabel('y'); zlabel('Z'); title('Peaks');
63
Matlab’s response:
Peaks
8
6
4
2
0
Z
-2
-4
-6
-8
4
2
2
1
0
0
-2
-4
y
-1.5
-1
1.5
0.5
-0.5
-2
x
Peaks
8
6
4
2
0
Z
-2
-4
-6
-8
4
2
1
0
0
-2
y
-4
-2
-1.5
-1
1.5
2
0.5
-0.5
x
Comments:
Creating the 3D mesh and a 3D surface with a higher density
meshgrid.
64
To find what other useful commands can be accompanied the me sh and surf
commands, use the online help.
3.2.2.1 Examination of a Function’s Critical Points
Many times, a researcher is faced with an unconstrained optimization
problem. Than is, it has a two variable function Z=f(x,y) and wants to
examine this function in a certain area in order to locate any minimum,
maximum or saddle point(s). From the previous section, it is apparent that
in the range [-10,10] the peaks function seems to have various critical
points. In optimization theory, a critical point can be located via the use of a
contour plot. A contour plot depicts the level curves of f(x,y) for some values
V. In other words, we project the sections/incision of various heights of the
Z=f(x,y) function in the (x,y)-plane. Matlab offers such function named as:
contour. Experiment with the following code to see the usefulness of contour
plots.
Matlab’s command:
>> V=-10:1:10; [c,h] = contour(x,y,Z,V); clabel(c,h), colorbar; hold
on;
>> xlabel('x'); ylabel('y'); title('Contour plot of the peaks function');
Matlab’s response:
Contour plot of the peaks function
4
6
3
1
1
2
1
0
4
1
3
-1
1
2
2
Local Maximum
1
-3
-2
3
Local Maximum
1
0
-1
-2
-3
-4
-5
Global
Minimum
-6 -5
-3
-4
-2
0-1
-2
2
2
2
0
4
3
Global Maximum 4
5
6
3
2
1
Local Minimum
0
-2
1
-1
6
7
7
3
-1
-2
y
45
5
0
2
3
2
0
2
1
0
-2
-1
-1
-3
-4
-2
-4
0
-1.5
-1
-0.5
0
x
0.5
1
1.5
2
-6
65
Comments:
Creating the contour plot of the peaks function. Viewing this plot,
it is easy to identify the critical points of the function. There is
one global maximum, one global minimum, two local maxima and
a local minimum. Additionally, from the color-bar that is created
with the command: col orbar, and from the values printed next to
the contour curves, it is obvious that the peaks functions around
its critical points exhibits a flatness (saddle points) (Note: the “*”
that indicate a critical point are plotted approximately); the text
next to each critical point was placed with the gte xt command.
Alternatively, we can approximate the maximum of the peaks function by
searching exhaustively the Z matrix (to do so, we should re-define the x and
y vectors to have high dense). This is done with the following code:
Matlab’s command:
>> close all; x=-2:0.05:2; y=-4:0.25:4; [X,Y]=meshgrid(x,y);
>> Z =3*(1-X).^2.*exp( -(X.^2) - (Y+1).^2)- ...
10*(X/5-X.^3-Y.^5).*exp( -X.^2-Y.^2)-1/3*exp( -(X+1).^2-Y.^2);
>> V=-10:1:10; [c,h] = contour(x,y,Z,V); clabel(c,h), colorbar; hold
on
>> xlabel('x'); ylabel('y'); title('Contour plot of the peaks function');
>> Fmax=max(max(Z)); P=find(Z==Fmax); xy=[X(P) Y(P)];
>> plot(xy(1),xy(2),'rp', 'MarkerSize',10);
>> text(xy(1)+0.05,xy(2), 'Maximum Point');
Matlab’s response:
Contour plot of the peaks function
4
6
3
1
2
2
0
4
-1
-2
3
2
0
2
1
-1
2
3
1
0
2
-5
-4
2
0
1
-1
-2
1
3
2
-2
0
2
1
3
0
0
-1
3
1
-3
y
4
Maximum Point
5 4
6
7
5
1
3
5
7
6
1
1
4
3
2
-3
0
-1
0
-2
-3
-6
-2
-5
-4
-3
-2
-1
-2
-1
-4
-3
0
-4
-2
-6
-1.5
-1
-0.5
0
x
0.5
1
1.5
2
66
Comments:
Locating the maximum of the peak function via an exhaustive
search. “Fmax=max(max(Z))” stores in F max the maximum value
of the Z matrix that is equal to 7.9966. “P=fi nd(Z==Fmax)” returns
in P the element index (a single value) where Z is equal to Fmax;
specifically the Z element with index number 1343 has the value
of 7.9966. Finally, in xy we store the x-and-y coordinates of the
maximum point. “Marke rSi ze ” in the pl ot command creates a
lager size mark symbol.
For practice try to write your own code to find the global minimum of the
peaks function (you can also try to find the local minima and maxima but
this is tricky).
67
Fourth Section
4. Control Flow
A collection of commands that include repetition of a conditional code
segment is termed as control flow structure. In Matlab as in any
programming language, control flow commands are presented via the
execution of a conditional expression (e.g. execute a code segment if a
statement is true) that is based on logical and/or relational operators.
4.1. Logical and Relational Operators
To evaluate a conditional code, it is needed to have a Boolean expression
that takes two possible values: TRUE or FALSE. Matlab defines a TRUE
statement with the value of 1 and a FALSE with the value of 0. In Matlab
there are six relational operators: “<” (less than), “<=” (less than or equal to),
“>” (greater than), “>=” (greater than or equal to), “==” (equal to), and “~=”
(not equal to). These can be used to compare a variable to a scalar, a vector
to a vector or a multidimensional array to another one. Always the
comparisons are done element by element and the result is a
scalar/vector/matrix of the same size as then ones originally used, with
elements set to one where the relation is true and elements set to zero where
it is not.
In addition, Matlab has (at least) 3 logical operators: “&” (logical AND), “|”
(logical OR), and “~” {logical complement - not). If we have two matrices “A”
and “B” that share the same dimensionality then:
•
“A” & “B” is a matrix whose elements are 1's where both “A” and “B”
have non-zero elements, and 0's where either has a zero element. “A”
and “B” must have the same dimensions (or one can be a scalar). For
example in the case of scalars: 1 & 0, 0 & 1 and 0 & 0 will result to 0
(FALSE) while 1 & 1 is 1 (TRUE).
•
“A” | “B” is a matrix whose elements are 1's where both “A” or “B” has
a non-zero element and 0's where both have zero elements. “A” and
“B” must have the same dimensions (or one can be a scalar). For
68
example and for the case of a scalar: 0 | 1, 1 | 0, and 1 | 1 is 1
(TRUE) while 0 | 0 is 0 (FALSE).
•
“~A” is a matrix whose elements are 1's where “A” has zero elements
and 0's where “A” has non-zero elements. For example and in the
case of a scalar: ~1 is (FALSE) and ~0 is 1 (TRUE).
Note that for Matlab, any number (integer or real, positive or negative)
different from 0 (zero) is a true statement, that is, it has the same meaning
as with 1. Pay also attention that the precedence with relational and logical
operators is the following (from highest to lowest):
1. Transpose “ .' ”, power “.^”, complex conjugate transpose “ ' “,
matrix power “^”;
2. Unary plus “+”, unary minus “-“, logical negation “~”;
3. Multiplication “.*”, right division “./”, left division that returns the
inverse of a division “.\”, matrix multiplication “*”, matrix right
division “/”, matrix left division “\”;
4. Addition “+”, subtraction “–”;
5. Colon operator “:”;
6. Less than “<”, less than or equal to “<=”, greater than “>”, greater
than or equal to “>=”, equal to “==”, not equal to “~=”;
7. Element-wise logical AND “&”;
8. Element-wise logical OR “|”.
View the examples that follow to digest the use or logical and relational
operators.
Matlab’s command:
>> clear all; x=2; y=0; z=-2;
>> a=(x>=1), b=(x~=1 & y), c=(1|y & x>0), d=(~y & z | ~x == 5)
Matlab’s response:
a=
1
b=
0
c=
1
69
d=
1
Comments:
Logical and relational operations. a is 1 because the statement
evaluated is TRUE since x is 2 and greater than 1. b is FALSE
because: “x~=1” returns 1, and “1 & y” returns 0. c is TRUE
because: “x>0” is 1, and “1|y & 1” is “ 1 | 1” which is TRUE. d is
TRUE because: “~y” is 1 and “~x” is 0 so we have “(1 & z | 0==5)
that is equal to “(1 & z | 0) that is equal to: “1 | 0” that is TRUE.
Some examples with matrices and the logical and relational operators follow:
Matlab’s command:
>> clear all; x=[5 0 -1; 2 4 8]; y=[2 1 -1; 1 2 4];
>> a=(x==5), b=(x~=1 & y), c=(2*y==x | ~x), d=(x>0 | y==1 |x~=x)
Matlab’s response:
a=
1
0
0
0
0
0
1
1
1
1
1
1
0
1
1
1
0
1
b=
c=
d=
1
1
0
1
1
1
Comments:
Logical and relational operations with matrices. In a we have only
the first element to be 1 since it the only one that is equal to 5.
We get b to be a TRUE matrix because “x~=1” returns a matrix of
1’s since none element is equal to 1. By definition, all elements in
y are taken to be TRUE statements. So TRUE & TRUE gives b full
of 1’s (Figure out how the c and d were evaluated).
4.1.1 The any and all Functions
Matlab has two build-in functions that are work as logical operators. The first
one is the any function that is TRUE if any element of a vector is nonzero.
For vectors, any returns 1 if any of the elements of the vector are non-zero.
Otherwise it returns 0. For matrices, any operates on the columns of the
70
matrix, returning a row vector of 1's and 0's. The second one, al l , becomes
TRUE if all elements of a vector are nonzero. For vectors, al l returns 1 if
none of the elements of the vector are zero. Otherwise it returns 0. For
matrices, al l operates on the columns of the matrix, returning a row vector
of 1's and 0's. View the following code to understand these tow functions.
Matlab’s command:
>> clear all; z=[-5 2 0]; x=[5 0 -1; 2 4 8]; y=[2 1 -1; 1 2 4];
>> a1=any(z), a2=any(x), a3=any(y), a4=all(z), a5=all(x), a6=all(y)
Matlab’s response:
a1 =
1
a2 =
1
1
1
a3 =
1
1
1
0
1
a4 =
0
a5 =
1
a6 =
1
1
1
Comments:
Displaying the use of any and al l .
4.2. Conditional Statements
The above section has been introduced since it is necessary for the
evaluation of conditional statements as well as loop expressions (see the
following section). A conditional statement is a segment of programming
code that evaluates a statement; if the statement is TRUE then it executes
some commands, otherwise if it is FALSE it runs a bulk of different
programming code. The two most important conditional statements that
Matlab materialize, is the i f statement and the swi tch statement.
71
4.2.1 The if Statement
The i f statement evaluates a logical expression and executes a group of
statements when the expression is TRUE. The optional e l se i f and e l se
keywords can be used for the execution of alternate groups of statements.
An e nd keyword, which matches the i f, terminates the last group of
statements. The groups of statements are delineated by the four above
keywords-no braces or brackets are involved [2]. The three possible syntax
versions of this conditional expression are tabulated in Table 7.
Syntax
if logical expression
segment of programming code executed
if the logical expression is TRUE
end
if logical expression
segment of programming code executed
if the logical expression is TRUE
else
segment of programming code executed
if the logical expression is FALSE
end
if logical expression #1
segment of programming code executed
if the logical expression #1 is TRUE
elseif logical expression #2
segment of programming code executed
if the logical expression #2 is TRUE
else
segment of programming code executed
if the previous logical expressions are
FALSE
end
Example
flag=1;
if ~isempty(flag)
disp('Hello')
end
sales=5000;
if sales<1000
Profit=sales*0.1;
else
Profit=(sales-1000)*0.2+1000*0.1;
end
sales=5000;
if (sales>1000 & sales<=2000)
disp('Low Sales');
Profit=sale*0.1;
elseif (sales>2000 & sales<=10000)
disp('Medium Sales ');
Profit=sales*0.15;
else
disp('Satisfactory Sales ');
Profit=sales*0.17;
end
Table 7: The i f statement syntax and examples.
72
Although is possible to run these examples via the command window, it is
better to use the Matlab Editor/Debugger to write a script instead. Real
examples with the conditional statements as well as with the loops are
postponed until the introduction of scripts in section 5.
4.2.2 The sw itch Statement
The swi tch statement executes groups of statements based on the value of a
variable or expression. The keywords case and othe rwi se delineate the
groups. Only the first matching case is executed. There must always be an
e nd to match the swi tch. [2]. The expression following the case should be
either a scalar or a string. The syntax of this conditional expression is
tabulated in Table 8.
Syntax
Example
switch expression
dice=3;
switch (dice)
case choice #1
case 1
disp('One')
segment of executable programming code
case 2
disp('Two')
case choice #2
case 3
disp('Three')
segment of executable programming code
case 4
disp('Five')
otherwise
case 5
disp('Five')
segment of executable programming code
otherwise
disp('Six')
end
end
Table 8: The swi tch statement syntax and example.
4.3. Loop Expressions
As mentioned before, loop statements are useful when a segment of
executable programming code is needed to be executed either a specific
number of times, than or as long as an expression is TRUE. The for and
whi l e loop statements are needed commands when writing efficient
programming code.
73
4.3.1. The for Loop
The for loop repeats a group of statements a fixed, predetermined number of
times. A matching e nd delineates the statements. The syntax for the for loop
is exhibited in Table 9.
Syntax
for index=first_value:step:last_value
segment of executable programming code
Example
for i=1:10
disp(i)
end
sumj=0;
for j=25:-2:-12
sumj=sumj+j;
end
Table 9: The for statement syntax and example.
end
The colon notation is similar as in the case of the vectors. Actually, index in
the for syntax is a vector with n elements with first element being the
first_value and last the last_value. The difference between the index
elements is step. Afterwards, the for statement executes n times the segment
of executable programming code moving from the first element of the index
to the last one element-by-element at each time. If step is not displayed,
then by default is set to 1.
4.3.2. The while Loop
The whi l e loop repeats a group of statements an indefinite number of times
under control of a logical condition. That is, as long as an expression is
TRUE, then the segment of executable programming code that is included in
the whi l e statement is executed. A matching e nd delineates the statements
[2]. The syntax for the whi l e loop is exhibited in Table 10.
Syntax
while expression
segment of executable programming code
end
Example
X=-3;
while X<=10
disp(X)
X=X+1;
end
Table 10: The whi l e statement syntax and example.
74
4.3.3. Nested Conditional and Loop Expressions
All conditional and loop statements can be combined in any way that is
desirable. If for example a loop expression includes an i f statement that
nests a swi tch statement and so on, then, in programming terminology, it is
termed that we have nested statements. As long as the statements are
nested in a logical and a non redundant manner, the user will get correct
answers. View the following example that is exhibited in Table 11 and nests
various statements (figure out their use).
An example of syntax of nested conditional and loop statements
clear; flag=1; x=2*pi; temp=pi;
while x<=4*pi
figure; hold on;
X=temp:pi/10:x;
for j=1:4
subplot(2,2,j); plot(X,sin(j*X)./X, 'b:', 'LineWidth', 3);
switch (j)
case 1
title('Plot of y=sin(x)/x');
case 2
title(' Plot of y=sin(2x)/x');
case 3
title(' Plot of y=sin(3x)/x');
otherwise
title(' Plot of y=sin(4x)/x');
end
xlabel('x'); ylabel('y');
end
temp=x; x=x+pi;
end
Table 11: Nested conditional and loop statements.
4.3.4. Additional Control Flow Statements
Matlab has additional control flow statements that can be used to write an
executable script or function. These are more specialized statements that are
listed in Table 12. You can learn more details via the online help.
75
Statement
bre ak
Comment
Terminates the execution of a for or whi l e loop.
Statements in the loop that appear after the bre ak
statement are not executed.
conti nue
Passes control to the next iteration of the for or while
loop in which it appears, skipping any remaining
statements in the body of the loop.
t r y … ca t ch
Changes flow control if an error is detected during
execution.
re turn
Causes a normal return to the invoking function or
to the keyboard. It also terminates keyboard mode.
Table 12: Additional control flow statements.
76
Fifth Section
5. m-files: Scripts and Functions
Up to this point, all commands passed to Matlab, were done through the
command window. But when a segment of programming code is composed
from several different commands, then it is time consuming, inefficient and
quite difficult to continue using the command window. To alleviate this
peculiarity, Matlab allows for the creation of functions and scripts by using
an Editor/Debugger that looks like a text editor.
As said, functions and scripts can be created with the use of the Matlab’s
Editor/Debugger. You only have to write the command lines, save the file in
a directory of your choice and execute it by typing its name to the command
window and pressing [Enter] (you have to make sure that the Matlab’s
current directory and the directory in which you save the file are the same).
Although m-files represent a text file and it is possible to use any text editor
to create a function or a script (as long as the extension of the file is *.m this
can work), it is preferable to use the default editor because: i) when you save
a file it automatically takes the extension *.m, ii) the reserved words like: for,
whi l e , functi on, e nd etc are bl ue colored whilst comments that make the
programming code more readable are green colored, and iii) it automatically
communicates with the command window and allows to run a script via a
command found in the Debug menu (see the menu bar of Editor/Debugger).
5.1 m-files: Functions
Functions are m-files that can accept input arguments and return output
arguments. The name of the m-file and of the functi on should be the same.
Functions operate on variables within their own workspace, separate from
the workspace you access at the Matlab command prompt. Functions are
useful for extending the existing Matlab language for personal applications
For example a practitioner might want to write various functions that return
77
the theoretical price of a call option contract according to various options
pricing models. Options pricing models like the Black and Scholes, the
Merton’s Jump’s diffusion, the displaced diffusion model, Heston’s
stochastic volatility model, and other can easily be implemented via a
different function.
A simple example of a function named as DiagExtract.m that takes as input a
square matrix and returns in a vector the elements of its main diagonal is
exhibited in Figure 12.
Figure 12: An example of a function
For the function Di agExtract note the followings: i) if after executing your
function you get an error, then read the error message that it is returned to
the command window (this is very helpful in finding where to look for the
78
error); you have to return to the Editor to debug the error, re-save the
function and try to run it again. If you debug your function or add something,
then you have to re-save the file in order to take place the changes (note that
if unsaved changes are made in a function file, an asterisk (*) appears next
to the function name in the Editor’s title bar (so in Figure 12, the functions
has not been saved); ii) although the input argument of the function is a
matrix named X and the output is a vector named V , when you call this
function from a script or from the command window, you can give any names
you like. For example in the command window enter:
“[DiagElements]=DiagExtract(magic(4))”
to see the result; iii) After the function is executed, none of the variables that
were used are save d in the workspace; iv) If after each command line you do
not place the semi-colon “;” then when the function is executed, you can
observe in the command window the result of these command lines (this is
useful to be done when you try to debug a function); v) observe on Figure 12
that on the bottom of the Editor/Debugger there is a predefined caption area
that indicates that the current m-file is a function with the name
Di agExtract.
5.1.1 Basic Parts of a Function
A function is composed from the following parts (most of this section is
taken/copied from [2])
5.1.1.1 Function Definition Line
The functi on definition line informs Matlab that the m-file contains a
functi on, and specifies the argument calling sequence of the function. For
example, the functi on definition line for the ave rage function (that computes
the average of a vector) could be:
79
(Figure copied from [2])
Matlab function names have the same constraints as variable names. The
name must begin with a letter, which may be followed by any combination of
letters, digits, and underscores. Making all letters in the name lowercase is
recommended as it makes your m-files portable between platforms (of course
the use of upper case assures that the functions names you create do not
resemble any other Matlab function and/or reserved word). The name of the
text file that contains a Matlab function consists of the function name with
the extension .m appended. For example, “DiagExtract.m”.
If the filename and the function definition line name are different, the internal
( functi on) name is ignored. Thus, if “DiagExtract.m” is the file that defines a
function named: di agonal _ e xtracti on, you would invoke the function by
typing in the command window:
“Di agExtract”
Concerning function arguments, if the function has multiple output values,
enclose the output argument list in square brackets “[ ]”. Input arguments, if
present, are enclosed in parentheses “( )”. Use commas to separate multiple
inputs or output arguments. Here's a more complicated example:
“functi on [Abs, Mean, Std] = Stati sti S(X, Y, Z)”
If there is no output, leave the output blank:
“functi on pri nt_ re sul ts(x)”
or use empty square brackets:
80
“functi on [] = pri nt_ re sul ts (x)”
The variables that you pass to the function do not need to have the same
name as those in the function definition line.
5.1.1.2 The H1 Line
The H1 line, so named because it is the first help text line, is a comment line
immediately following the functi on definition line. Because it consists of
comment text, the H1 line begins with a percent sign, "%." For the
Di agExtract, the H1 line is:
“% DiagExtract returns the diagonal elements of a square matrix (not single values).”
This is the first line of text that appears when a user types he l p
function_name at the Matlab prompt. Further, the l ookfor searches and
displays only the H1 line of the functions. Because this line provides
important summary information about the m-file, it is important to make it
as descriptive as possible.
5.1.1.3 The Help Text
You can create online help for your m-files by entering text on one or more
comment lines beginning with the line immediately following the H1 line. The
help text for the Di agExtract function is:
“%
%
%
%
%
This function takes as input a square matrix named X and does the followings:
1. If by mistake the user does not enter a square matrix, it returns
an error message
2. If a square matrix is correclty entered, then it returns the
elements of its main diagonal in vector V ”
When you type he l p function_name, Matlab displays the comment lines that
appear between the function definition line and the first non-comment
(executable or blank) line. The help system ignores any comment lines that
appear after this help block.
81
5.1.1.4 The Body Text
The function body contains all the Matlab code that performs computations
and assigns values to output arguments. The statements in the function
body can consist of function calls, programming constructs like flow control
and interactive input/output, calculations, assignments, comments, and
blank lines.
For example, the body of the Di agExtract function contains a number of
simple programming statements:
“%
Author: Panayiotis Andreou, Sept. 2003
%
This function uses the error build-in function that displays a message
%
and aborts the function's execution
[m n]=size(X); %Saving the size of the matrix
if isempty(X) %Checking if it is an empty matrix
error('You have not passed a square matrix');
elseif (m~=n) %Checking if matrix is square
error('You have enter a non square matrix');
elseif (m==n & m==1) %Checking if it is a single value
error('You have enter a single value');
else
Ind=(1:n:n^2)+(0:n-1); %Finding the indeces of the diagonal elements
V=X(Ind); %Extracting to V the diagonal elements
end ”
5.2 Scripts
On the other hand, scripts can operate on existing data in the workspace, or
they can create new data on which to operate. Although scripts do not
return output arguments, any variables that they create remain in the
workspace, to be used in subsequent computations. In addition, scripts can
produce graphical output using functions. Scripts are useful for automating a
series of steps that are needed to be performed many times (e.g. to create a
82
script that calls various options pricing function in order to price a call option
and compare the pricing accuracy of each model).
Unlike functions, a script has no a specific structure. It includes a number of
commands that are serially executed. As long as the command series has a
logical interpretation, the script will result to the desire output. Remember
that a script does not take and does not return input and output arguments
respectively. The vectors and matrices (variables or scalars) are stored in the
Matlab’s workspace. An example of a script follows.
Let’s say that we need to create a script with the name “CompuStat.m” that
should store in a vector named Data, the mean, standard deviation, median,
covariance, minimum and maximum of the main diagonal of a magic square.
Figure 13, shows how a version of such a script might look like for an 8-by-8
magic square.
Figure 13: An example of a script
83
Try to see what this script does. After executing the script, figure out what is
the difference between the command di sp and the fpri ntf. Use the command
who to view the script’s variables that are saved in the workspace. Notice
that a script does not has the same structure as a function. Moreover,
observe on Figure 13 that on the bottom of the Editor/Debugger there is a
predefined caption area that indicates that the current m-file is a script.
Important Note: when you start writing scripts and functions that are
stored in a certain directory, you occasional need to see what files are
included in this directory. To do so, from the command window you can use
the di r command (the same one as used in the MS-DOS) to view the
contents of Matlab’s current directory or what to view all m-files in the
directory. Additionally, you can use cd directory_name to set the current
directory to the one specified and cd .. to move to the directory above the
current one. Moreover, de l e te file_name deletes the specified file, and pwd
prints on the screen the current directory.
84
Sixth Section
6. Cells and Structures
Structures are collections of different kinds of data organized by named
fields. Cell arrays are a special class of Matlab arrays whose elements
consist of cells that themselves contain Matlab arrays. Both structures and
cell arrays provide a hierarchical storage mechanism for dissimilar kinds of
data. They differ from each other primarily in the way they organize data.
You access data in structures using named fields, while in cell arrays data is
accessed through matrix indexing operations [2].
6.1 Cells
A cell array is a Matlab array for which the elements are cells, containers
that can hold other Matlab arrays. For example, one cell of a cell array might
contain a real matrix, another an array of text strings, and another a vector
of complex values [2]. Moreover, you can build cell arrays of any valid size or
shape, including multidimensional structure arrays. Figure 14 gives an
illustration on how a 2-by-2 cell array might look.
cell (1,1)
cell (1,2)
NaN
5
Inf 3 + 5i
cell (2,1)
' My name is Panayiotis'
' Yours ?'
cell (2,2)
cell (1,1)
[]
[]
cell (1,2)
'Hello World'
cell (2,1)
cell (2,2)
[1 2 5 6]
5 NaN
Inf 3 + 5i
Figure 14: A 2-by-2 cell array
85
To create a cell array use the command: ce l l . For example if we want A to be
a 3-by-3 cell array, then you should use the following syntax:
“A=ce l l (3,3)”
to get:
“A =
[]
[]
[]
[]
[]
[]
[]
[]
[] “
That is, the A has been created to be a 3-by-3 empty cell array. The cells
identification is the same as with matrices. The upper left cell
location/position is (1,1), the next cell in the same row is (1,2) and so on
(single value indexing is allowed also). You can fill a cell array by assigning
data to individual cells one at a time always supporting the correct cell
location/index. Matlab has two default ways to store data (scalars, vectors,
matrices, strings, cells, etc) to cells:
Cell indexing
Enclose the cell subscripts in parentheses using standard array notation.
Enclose the cell contents on the right side of the assignment statement in
curly braces, "{ }" [2]. For example:
“A(1,1) = {[1 4 3; 0 5 8; 7 2 9]}; A(1,2) = {'Anne Smith'};
A(2,1) = {3+7i}; A(2,2) = {-pi:pi/10:pi}; A(2,3)={5};
G=cell(2,1); G(1,1)= {[5 6 9]}; G(2,1)={'Hello World'};
A(3,1) = {G}; A(3,3)={ones(2,2)}; ”
After assigning the cells, in the command window type: “A” to get:
86
“A =
[3x3 double]
'Anne Smith'
[3.0000+ 7.0000i]
[1x21 double]
{2x1 cell }
[]
[
[]
5]
[2x2 double] ”
Content indexing
Enclose the cell subscript s in curly braces using standard array notation.
Specify the cell contents on the right side of the assignment statement [2].
For example:
“A{1,1} = [1 4 3; 0 5 8; 7 2 9]; A{1,2} = 'Anne Smith';
A{2,1} = 3+7i; A{2,2} = -pi:pi/10:pi; A{2,3}=5;
G=cell(2,1); G{1,1}= [5 6 9]; G{2,1}='Hello World';
A{3,1} = G; A{3,3}=ones(2,2); ”
produces the same cell array as before.
If you assign data to a cell that is outside the dimensions of the current
array, Matlab automatically expands the array to include the subscripts you
specify. It fills any intervening cells with empty matrices. For example, the
assignment below turns the 3-by-3 cell array A into a 3-by-4 cell array [2]
(note that the same holds for vectors and matrices with the only difference
that empty elements are assigned with zero values).
“A{3,4}='This expands the cell array';”
to get:
“A =
[3x3 double]
'Anne Smith'
[3.0000+ 7.0000i]
[1x21 double]
{2x1 cell }
[]
[
[]
[]
5]
[]
[2x2 double]
[1x27 char]”
87
The only difference between the ce l l command and the cell and content
indexing is that by using ce l l you pre-allocating the cell’s dimensions.
You can use content indexing on the right side of an assignment to access
some or all of the data in a single cell. Specify the variable to receive the cell
contents on the left side of the assignment. Enclose the cell index expression
on the right side of the assignment in curly braces. This indicates that you
are assigning cell contents, not the cells themselves. For example, to store to
B the 3-by-3 matrix that is located in A(1,1), you should do the following:
“B=ce l l {1,1};”
to get:
“B =
1
4
3
0
5
8
7
2
9”
and to save in C the 2nd and 3rd elements of the vector that is saved in the
(1,1) cell of G which is saved in the (3,1) cell of A you do the following:
“C= A{3,1}{1,1}(2:3)”
to get:
“C =
6
9”
If you like to save in D the cells (1,2) to (2,3) of A (that is to create a 2-by-2
cell array) you do the following:
“D=A(1:2,2:3)”
to get:
“D =
'Anne Smith'
[]
88
[1x21 double]
[5] ”
So, if “{ }” are used after a cell array then Matlab returns the array’s contents
but if “( )” are used instead, then it returns cells. To access sub-sets of
information stored in a cell use first “{ }” to access the cell and after used “( )”
to access the info you want.
Before leaving this section, notice the existence of two very useful cell arrays
functions. These are: ce l l di sp that recursively displays the contents of a cell
array, and ce l l pl ot displays the structure of a cell array as nested coloured
boxes. Further info for cell arrays can be obtained from the Matlab’s online
help facilities.
6.2 Structures
Structures are Matlab arrays with named data container" called fields. The
fields of a structure can contain any kind of data. For example, one field
might contain a text string representing a name, another might contain a
scalar representing a billing amount, a third might hold a matrix of medical
test results, and so on. Like standard arrays, structures are inherently array
oriented. A single structure is a 1-by-1 structure array, just as the value 5 is
a 1-by-1 numeric array. You can build structure arrays with any valid size or
shape, including multidimensional structure arrays (see figure below) [2].
(Figure copied from [2])
Structures can be created either by using assignment statements or by
using the struct function.
89
Building structure arrays using assignment statements
You can build a simple 1-by-1 structure array by assigning data to individual
fields. Matlab automatically builds the structure as you go along. For
example, create the 1-by-1 patient structure array shown at the beginning of
this section [2]:
“patient.name = 'John Doe';
patient.billing = 127.00;
patient.test = [79 75 73; 180 178 177.5; 220 210 205]; “
and if you type: “patient” in the command window you get:
“patient =
name: 'John Doe'
billing: 127
test: [3x3 double] ”
that is an array containing a structure with three fields. To expand the
structure array, add subscripts after the structure name:
“patient(2).name = 'Ann Lane';
patient(2).billing = 28.50;
patient(2).test = [68 70 68; 118 118 119; 172 170 169];”
and if you again type: “patient” you will get:
“patient =
1x2 struct array with fields:
name
billing
test ”
The patient structure array now has size [1 2]. Note that once a structure
array contains more than a single element, Matlab does not display
90
individual field contents when you type the array name. Instead, it shows a
summary of the kind of information the structure contains.
You can also use the fi e l dname s function to obtain this information.
fi e l dname s returns a cell array of strings containing field names (see the
online help).
As you expand the structure, Matlab fills in unspecified fields with empty
matrices so that:
•
All structures in the array have the same number of fields
•
All fields have the same field names
For example, entering “patient(3).name = 'Alan Johnson' ” expands the
patient array to size [1 3]. Now both “patient(3).billing” and “patient(3).test”
contain empty matrices. To see this, type: “patient(3)” to get:
“ans =
name: 'Alan Johnson'
billing: []
test: [] ”
Building structure arrays using the struct function
You can pre-allocate an array of structures with the struct function. Its basic
form is [2]:
“str_array = struct ('field1',val1,'field2',val2, ...)”
where the arguments are field names and their corresponding values. A field
value can be a single value, represented by any Matlab data construct, or a
cell array of values. All field values in the argument list must be of the same
scale (single value or cell array). To create the structure with the patient info
shown before you should have the following syntax (the first command line
instructs for the creation of a 1-by-3 structure will all fields set to empty):
“patient(3)= struct ('name',[],'billing',[],'test',[]);
91
patient(1)=struct('name', 'John Doe', 'billing', 127.00, 'test', ...
[79 75 73; 180 178 177.5; 220 210 205]);
patient(2)=struct('name', 'Ann Lane', 'billing', 28.50, 'test', ...
[68 70 68; 118 118 119; 172 170 169]);
patient(3)=struct('name', 'Alan Johnson', 'billing', [], 'test', []);”
The view an entire field this can be done with the following example syntax:
“structure_name.field_name”
For example type: “patient.name” in the command window to get:
“patient.name
ans =
John Doe
ans =
Ann Lane
ans =
Alan Johnson ”
To view the fields data associated with a certain structure entry, the calling
syntax should be of the form:
“structure_name(index_of_entry)”
For example type: “patient(2)” in the command window to get:
“ans =
name: 'Ann Lane'
billing: 28.5000
test: [3x3 double] ”
To manipulate sub-data on data stored under a fields name for a specific
entry, the calling syntax should be of the form:
92
“structure_name(index_of_entry).field_name( ) ”
For example type: “patient(2).test(2:end,1:end-1)” in the command window to
get:
“ans =
118 118
172 170 ”
Useful build-in functions that can make the structures handling much easier
include:
•
fi e l dname s to get structure field names
•
ge tfi e l d that can be used to get structures’ fields
•
i sfi e l d that returns a TRUE if field is in structure array
•
rmfi e l d that can be used to delete a structure’s field
•
se tfi e l d that can be used to assign a structure field
Structures and cell arrays are very useful when you need to write a program
that handles various data types. It is a challenge to work with such data
types. Before attempting writing a segment of programming code based on
these make sure that you have spent a lot of time reading the Matlab’s
online help.
93
Seventh Section
7. Entering and Saving Data Files
Matlab can be used to both load a file of data from an external source and to
save to your PC data-sets that are located in the workspace or that are
created from a function. When you have to deal with small amount of data,
then you can enter them by hand either in the command window or in the
Editor/Debugger. But when you have to work with a large amount of data
retrieved by an external source (e.g. you need to process the historical daily
prices for S&P 500 from 1985 to 1999, saved in a file that was downloaded
from the Internet), then it is an imperative need to use some build-in
functions that can read files of data. Although there are different commands
that can load in workspace various types of data files, we review the two
most important ones.
7.1. Reading Text ASCII Files: The load command
l oad is extremely useful command for retrieving from an external source a
text file in ASCII form. The general calling syntax of this command is:
“Data= l oad ('filename');
The filename is better to either have the extension *.txt or *.dat because if it
does not have any extension, then the l oad has a different interpretation (see
he l p l oad for further details). If the file you want to retrieve is in a different
location than the one that the Matlab’s current directory looks, then a
complete path name should accompanied this command, for example:
“Data = l oad (' c:\Documents\Functions\data.txt')”
If the l oad command is entered properly, then the contents of the ASCII file
will be stored in a matrix with the dimensionality of the data saved in the
ASCII file. In their simplest form, ASCII files contain rows and columns of
data separated by either a tab or a space. To be accessible by l oad the file
should not contain any text or missing values and all columns and rows
94
should have the same number of elements (of course the advance user can
handle via certain methodology missing values and text in an ASCII file).
To learn on how ASCII text data look, you can use Microsoft® Excel® that
can handle such data. For example, enter the following data (Figure 15) in a
new Excel® spreadsheet starting from cell (A1):
Figure 15: Excel® Data
Afterwards, go: File>Save As… and on the “Save As” window (Figure 16)
select a filename (e.g. random_number_data) for the data to be saved, choose
the directory you want to save (e.g. Matlab Examples) and moreover, on the
field “Save as type:” choose: “Text (Tab delimited)(*.txt)”.
95
Figure 16: Excel®’s Save As window
The data will be saved in a file with the name: “random_number_data.txt”
that can be loaded in Matlab. If by mistake, you save the file and there is an
entry at cell (A8), then when you attempt to l oad it you will get an error.
7.2 Saving Text ASCII Files: The save command
On the very opposite, when you need to save some data in a text file to be
able to access it later either by viewing it with Microsoft® Excel® or by reloading to Matlab, the user can use the save command. The general calling
syntax of the save is of the following form:
“save filename.ext variable_name options”
If a path is not provided with filename, this command saves the elements of
the variable_name in a file with the complete name filename.ext (where ext
stands for the extension of the filename and for consistency try to always use
.txt) in the current directory. If the scalar/vector/matrix (you cannot save cell
arrays or structures with this command unless first you extract their data in
a matrix or a vector variable) that is located in the workspace under the
96
name variable_name has components like: NaN or Inf, then these are saved
as text and not numbers in the saved txt file.
Concerning the options in the calling syntax, this can take the following
values for ASCII data saves (Table 13):
-ascii
-ascii -double
-ascii -tabs
-ascii -double -tabs
Table 13: Options
8-digit ASCII format
16-digit ASCII format
delimits with tabs
16-digit ASCII format, tab delimited
associated with save
The use of “–ascii” is common and satisfactory for most programming needs.
7.3 Other Reading and saving commands
Matlab can also read and save data in the following data formats (Table 14):
File Format
Extension
mat
Text
csv
dlm
tab
cdf
Scientific
Data
fits
hdf
Spreadsheet
xls
Wh1
File Content
Saved MATLAB
workspace
Comma-separated
numbers
Delimited text
Tab-separated text
Data in Common
Data Format
Flexible Image
Transport System
data
Data in
Hierarchical Data
Format
Read/save
Command
Returns
l oad/s ave
Variables in the
file
cs vre ad/cs vwri t e
Double array
dl mre ad/dl mwri t e
dl mre ad/dl mwri t e
Double array
Double array
Cell array of CDF
records
Primary or
extension table
data
cdfre ad
fi t s re ad
hdfre ad
Excel worksheet
xl s re ad
Lotus 123
worksheet
wk1re ad
HDF or HDFEOS data set
Double or cell
array
Double or cell
array
Table 14: File formats that Matlab can handle.
Use the “ he l p fi l e formats” to see the file formats that Matlab can handle, or
use the he l p to see the calling syntax of a certain read/save command.
97
Eighth Section
8. Case Studies
In the following sub-section, some very useful examples with functions and
scripts are illustrated. Read, implement and execute the codes that are
given. Try to change the code. Experiment by adding your own command
lines. Of course, for the needs of the course, you can find all needed
functions, scripts and datasets in the folder named as:
“Matlab Examples”
Depending on the place you are, this folder may be in different locations.
Send me an email or ask me in class for the exact location of this folder.
8.1 The Black – Scholes- Merton Options Pricing Formula
The Black Scholes Merton (BSM) model expresses the value of an option as a
function of the current value of a stock, S, the option’s strike price, X, the
option’s time to maturity, T, the volatility, s, of the stock price returns (this
is the standard deviation of the log-relative returns of the stock for the past
n days, where n is usually set equal to 60), the risk free rate, r, that prevails
for a maturity T and the stock’s dividend yield, d. The analytic formula for
the a European call option derived by BSM is:
c BSM = Se −dT N ( d 1 ) − Xe −rT N ( d 2 )
where,
d1 =
ln(S / X ) + ( r − d + s 2 / 2 )?
s T
,
d 2 = d1 − s T ,
and,
98
N( z ) =
1
x
∫
2p − ∞
1
− z2
e 2 dz
represents the cumulative normal distribution function with mean zero and
unity standard deviation (the Matlab build in function is named as:
normcdf).
The value of a European put option can also be defined via the BSM as:
p BSM = Xe −rT N ( −d 2 ) − Se −dT N ( −d 1 )
8.1.1 Implementation of the BSM Formula
We want to create a script named as OptionsBSM.m that calls the user
created function BSMpri ce to price European call, c, and European put, p,
options using the Black, Scholes and Merton model (BSM). The function
BSMpri ce should take seven (at least six) input parameters (as single values
or in the form of a vector) and should return the value (or the vector) of a
European call or put. Its calling syntax should look like:
“[Price] = BSMpri ce (S, X, T, vol, r, Index, dv)”
“Index” is a string input argument that is set as an additional input
argument that takes the values: 'CALL' (or any other spelling of the 'CALL'
such as 'Call', 'CaLL', etc), or 'PUT' (or any other spelling of the 'PUT' such as
'Put', 'PuT', etc) and should be used to define the kind of option type (use the
build in function l owe r to convert the “Index” to lower case). Note the “Index”
precedes “dv” because “dv” should be an optional input (will come back to
this in a while).
To validate the formula, via the script create a table that tabulates the call
and put values against the moneyness ratio, S, and maturity, T. The data
should be loaded from a text file (that the user creates either by hand or via
99
a function) named as “options_data.txt” in which the columns should contain
S, X, T, s, r, d. The data values are given below:
S = { 80, 85, 90 , 95, 100 , 105, 110, 115, 120 } ,
T = { 0.1, 0.15, 0.20, 0.25 }
s = { 0.1, 0.2, 0.3 }
and,
X = 100 , r = 0.05, d = 0.02
After creating the text file, you should have a 108-by-6 table since for each
value of T and s you have nine different possible values for S.
Note that the function:
•
Should check if the correct number of input arguments is supplied
and display an error massage otherwise (to do so, use the build-in
function nargi n; see the help facilities for understanding its use).
•
Set dividends equal to zero automatically if no dividend input is
supplied or if the dividend input argument is set to be an empty array
(use the build in function e xi st).
•
In order to prevent an error, the function should check whether the
input parameters are all positive or non-negative (elaborate on the
BSM formula to see which inputs should be >=0 and which only >0; d
and especially r with negative values can exist but do not have any
economical implication).
•
If “Index” takes a different value other than those explained before, an
error message should be returned and the program execution should
break. Additionally, an error should be returned and program
execution should stop if “Index” is a string matrix and not a string
vector (“Index” should be either 1-by-4 string vector in the case of a
'CALL' or a 1-by-3 in the case of a 'PUT').
100
8.1.2 BSM Derivatives
From the same script as above, call a function with the name: BSMde rivatives
that returns the partial derivatives of the BSM formula (known as the Greek
letters) for both the call and the put value. The partial derivatives are:
delta: ∂c / ∂S = N ( d 1 ) e −dT , ∂p / ∂S = −N ( −d 1 ) e −dT
theta: ∂c / ∂T = −
∂p / ∂T = −
n ( d 1 )S s
2 ?
n ( d 1 ) Ss
2 ?
gamma: ∂ 2c / ∂S 2 =
− rXe
+ rXe
n ( d1 )
Ss T
− rT
− rT
N (d2 )
N ( −d 2 )
, ∂ 2 p / ∂S 2 =
n( d 1 )
Ss T
vega: ∂c / ∂s = S T n ( d 1 ) , ∂p / ∂s = S T n( d 1 )
rho: ∂c / ∂r = XTe −rT N ( d 2 ) , ∂p / ∂r = −XTe −rT N ( −d 2 )
where,
n( z ) =
1
2p
2
e −z / 2
represents the normal probability density function with mean zero and unity
standard deviation (the build in function is named as normpdf). The
BSMde ri vati ve s calling syntax should be :
“[Derivatives] = BSMde ri vati ve s(S, X, T, vol, r, Index, dv)”
The function should make similar checks as before. The output of the
function BSMde ri vati ve s should be a row vector if the input arguments are
single values or a two dimensional array if the input arguments are vectors
with the following format:
“Derivatives=[Delta, Theta, Gamma, Vega, Rho]”
101
8.1.3 BSM Plots and Surfaces
Make the following plots:
•
Two subplot figures, one for call options with T=0.15 and s=0.20, and
one for put options with T=0.25 and s=0.20 that plot S against all
partial derivatives. Give titles and axis names.
•
A 3D surface of the cBSM and pBSM versus the S/X and T (note that in
order to create a smooth surface you should create a dense meshgrid) for the ranges:
80 ≤ S ≤ 120 , 0.10 ≤ T ≤ 0.25
for:
X = 100, s = 0.20, r = 0.05, d = 0.02
8.1.4 BSM Implied Volatility
The only unobservable parameter related with the BSM formula when we
deal with real world problems is the volatility measure, s (although as said
before it can be estimated via log-relative reruns of the underlying asset). It
is accustomed by options traders to observe a market value for a call or put
option and given the observed values of S, X, ?, r, and d, they derive the
value of s that equates the BSM estimate with the market quote. Such s
value is known as implied volatility. For instance, if cmrk is the market price of
a call option and S’, X’, T’, r’ and d’ are the observable parameters related
with the call option, then the BSM implied volatility, simp, is that value of s
that minimizes the absolute error between cmrk and cBSM. Analytically this
problem is:
min | g ( e ) |=| c mrk − c BSM ( S' , X ' ,T ' , s imp , r' , d' ) |
s imp
Alternatively, think this as solving the following equation:
c mrk = c BSM ( S , X , T , s imp , r , d ) |
102
for simp. It is known that such equation has no analytic solution, so to solve
it someone has to implement a numerical root-finding algorithm. The most
well known root finding algorithm for the implied volatility problem is the
Newton-Raphson method.
The Newton method is very simple and quite fast method. It can be
summarized in three steps:
0
•
Step #1: give an initial guess for s imp (e.g. s imp = 0.1 )
•
Step #2: perform an algorithm iteration, k, based on the following
formula:
k
s imp
=
k −1
simp
mrk
g( e )
− c BSM
k −1 c
−
= simp −
⇒
g' ( e )
∂c BSM
−
∂S
k
s imp
=
k −1
s imp
+
c mrk − c BSM
∂c BSM
∂S
for k=1,2,3,….
•
k
Step #3: If |g(e)|<e then stop and return s imp
, otherwise go to Step
#2 and perform one more iteration, k, of the algorithm (the e is the
desire accuracy, usually set to a very small quantity)
Write a function with the following calling syntax:
“[ImpliedVol]=BSMi mpl i e dV ol (Qmrk, S, X, T, r, Index, dv, maxNumIter, tol)”
where “Qmrk” is the market quote of a call or put option. “maxNumIter”
represents the number of iterations and “tol” the desire accuracy (it is a
stopping criterion related with the absolute difference of market option value
and BSM estimate). “Index” is a single string with values “CALL” and “PUT”
(or any other combination that delivers the required word meaning) that is
used to distinguish between calls and puts as before. Note that all input
103
arguments precede the optional ones (the optional are “dv”, “maxNumIter”
and “tol”).
Use as inputs the initial data from the loaded txt file (without considering s).
The function should make similar checking like previous functions with the
additional that:
•
If not specified, “maxNumIter” should be equal to 100.
•
If not specified, “tol” should be 1e-5.
•
At the beginning of the function, it should be tested whether with a
small value of s (e.g. s=0.001) the cBSM and pBSM are greater than cmrk
and pmrk respectively; if such condition holds (it can be observed in
practice as an arbitrage result), an implied volatility value that
minimizes |g(e)| does not exist, so the function should return a
“NaN” value.
•
To help the algorithm convergence rate and to save computing time,
the starting values for the algorithm should be given from the
following approximation suggested by Bharadia, Christofides and
Salkin [3]:
0
for call options: s imp
=
2p c mrk − d
, and,
? Xe − rT + d
0
for put options: s imp
=
2p p mrk + d
? Xe − rT + d
with,
d = 0.5( S − Xe −rT )
To use the implied volatility function, replace the volatility column of
the options data that were previously loaded from the text file with
random values taken from a uniform distribution on the interval [0,1]
(use the build in function: rand). Afterwards, use the BSMprice to find
the theoretical values for calls and puts. In the following, use the
BSMi mpl i e dV ol to verify that the implied volatility is quite close with
104
the ones that you have initially used (these are the random values) to
price calls and puts with the BSM. Note that the implied volatility of
calls and puts for should match for similar input arguments. Plot the
difference to visualize that always the dollar difference is less than
“tol” (given that the algorithm iterations were adequate to secure
convergence).
8.2 Function Minimization and Plots
There is a variety of optimization algorithms that can be used to minimize (or
to maximize) a univariate or a multivariate function (note that the
maximization of a function, f(x), is the same as the minimization of –f(x)).
Two well known and widely used algorithms are the gradient descent, that
minimizes a function by relying solely on a function’s first partial derivatives
(gradient vector), and the Newton’s descent algorithm that utilizes a
function’s second order partial derivatives (Hessian matrix).
The gradient descent algorithm can be summarized as follows:
•
Step #1: give an initial guess for the coordinates of the minimum point
x0 (e.g. if the function under consideration has two unknowns x1 and
0
0
x2, then x should be a two element row vector: x0=[ x 1 , x 2 ])
•
Step #2: perform an algorithm iteration, k, based on the following
formula:
x k +1 = x k − af ' ( x k )
for k=1,2,3,….
where f ( x k ) is the value of the function at kth iteration at point x and
f ' ( x k ) is a row vector that includes the first order partial derivatives of
f(.) w.r.t x’s at the kt h iteration. The parameter a is a positive scale
function that lies between 0 and 1 and is a learning rate that sets the
step size. Large values of a force the algorithm to oscillate around the
minimum point or even diverge, whereas small values of a lead to more
105
stable convergence but with extremely slow rate. Typical values of a
range between 0.01 and 0.15 depending on the faced problem.
Specifically, f ' ( x ) for a function with n variables is:
∂f ( x )
f ' ( x) =
∂x 1
•
∂f ( x )
∂x 2
L
∂f ( x )
∂x n
Step #3: Increase: k ← k+1 and if the current iteration index k is larger
than the maximum number of iterations or if af ' ( x k ) <e then stop and
return x k , otherwise go to Step #2 and perform one more iteration of
the algorithm (the e is the desire accuracy, usually set to a small
quantity such as 1e-6, whereas the maximum number of iterations
depends solely by the experience of the researcher).
The Newton Descent algorithm can be summarized as follows:
•
Step #1: give an initial guess for the coordinates of the minimum point
x0 (e.g. if the function under consideration has two unknowns x1 and
0
0
x2, then x should be a two element row vector: x0=[ x 1 , x 2 ])
•
Step #2: perform an algorithm iteration, k, based on the following
formula:
x k + 1 = x k − f ' ( x k )[ f ' ' ( x k )] −1
for k=1,2,3,….
where f ( x k ) is the value of the function at kth iteration at point x,
f ' ( x k ) is a row vector that includes the first order partial derivatives of
f(.) w.r.t x’s at the kt h iteration and [ f ' ' ( x k )] −1 is a square matrix that
represents the inverse of the second order partial derivatives of f(.) w.r.t
x’s (Hessian matrix) at the kt h iteration.
106
Specifically, f ' ' ( x ) for a function with n variables is:
∂2 f ( x)
∂x 12
2
∂ f ( x)
f ' ' ( x ) = ∂x 2 ∂x 1
M
∂2 f ( x)
∂x n ∂x 1
•
∂ 2 f ( x)
∂x 1 ∂x 2
∂ 2 f ( x)
∂x 22
M
2
∂ f ( x)
∂x n ∂x 2
∂2 f ( x )
∂x 1 x n
∂2 f ( x )
K
∂x 2 x n
M
M
2
∂ f ( x)
∂x n2
K
Step #3: Increase: k ← k+1 and if the current iteration index k is
larger
than
the
maximum
number
of
iterations
or
if
f ' ( x k )[ f ' ' ( x k )] − 1 <e then stop and return x k + 1 , otherwise go to Step
#2 and perform one more iteration of the algorithm (the e is the desire
accuracy, usually set to a small quantity such as 1e-6, whereas the
maximum number of iterations depends solely by the experience of the
researcher).
Both the gradient descent and the Newton descent algorithms have inherent
problems with their implementation. For example, the user should
“magically” define the correct value of the learning parameter a in order to
succeed a robust convergence of the algorithm when it comes to implement
the gradient descent algorithm, or concerning the Newton descent one, when
the Hessian matrix is singular and its inverse does not exist then it is not
applicable. Moreover, there is no way to secure that the initial point to set
up the algorithm will eventually help in reaching the minimum point. Most
of the times and when the user does not have a detail overview of the faced
problem, the initial value of x might be too far from the minimum point,
preventing in this way the algorithm to converge.
There are many suggestions to suppress these problems (i.e [4], [5]). In here,
we will implement these two algorithms just for getting the feeling on the
way that a minimization algorithm can be used. The user can later improve
the functions that will be illustrated according to his/her needs.
107
To implement the previous algorithms, the user should be in a position to
find the gradient vector and the Hessian matrix. Although it is better to work
with the exact first and second order partial derivatives of the function via
their functional form, a more flexible, practical and quite accurate way is to
create two functions in Matlab that calculate these with two sided finite
differencing methods. That is, instead of evaluating a function at a point x
by using the functional form of the gradient vector and the Hessian matrix,
it is easier to find these information via numerical differentiation (two sided
finite differencing).
The centred and evenly spaced finite difference approximation of the first
order partial derivatives (gradient vector) of a function f at point x is (for
simplicity assume a two variable function with x1 and x2 to be the unknown
variable – the extension to the n dimensional case is trivial):
∂f ( x )
∂x 1
∂f ( x )
∂x 2
≈
f ( x1 + h, x 2 ) − f ( x1 − h, x 2 )
2h
≈
f ( x1 ,x 2 + h ) − f ( x1 , x2 − h )
2h
where h is given from a rule of thumb (see [4] page 103),
h = max(| x |,1) 3 ∈
with ∈ to represent machine precision (this is the build-in function e ps).
The centred and evenly spaced finite difference approximation of the second
order partial derivatives (Hessian matrix) of a function f at point x is (for
simplicity assume a two variable function with x1 and x2 to be the unknown
variable – the extension to the n dimensional case is trivial):
∂f 2 ( x )
∂x 12
≈
f ( x 1 + 2h , x 2 ) + f ( x 1 − 2h , x 2 ) − f ( x 1 − 2h , x 2 ) − f ( x 1 + 2h , x 2 )
4h 2
108
∂f 2 ( x )
∂x 1 ∂x 2
≈
f ( x1 + h ,x 2 + h ) + f ( x1 − h ,x 2 − h ) − f ( x1 − h , x2 + h ) − f ( x1 + h , x2 − h )
4h 2
∂f 2 ( x )
∂x 1 ∂x 2
∂f 2 ( x )
∂x 22
≈
≡
∂f 2 ( x )
∂x 2 ∂x 1
f ( x 1x 2 + 2h ) + f ( x 1 x 2 − 2h ) − f ( x 1 x 2 − 2h ) − f ( x 1 x 2 + 2h )
4h 2
where h is given from a rule of thumb (see [4] page 103),
h = max(| x |,1) 4 ∈
Having in mind the above, write a script with the name: FunctionMin.m that
will do the following:
•
Make the 3D – surface and the contour plots of the function:
f ( x 1 , x 2 ) = e x ( 4 x 2 + 2y 2 + 4 xy + 2y + 1)
in the area − 2 ≤ x , y ≤ 1.5 . The function should be saved in an m-file
with the name: funToMi n. Given that you have created the m-file with
the functional form of the function, to evaluate it at a point use the
build in function: fe val . The calling syntax is:
“fe val (@funToMin,x)”
where x is a two element row vector (or m-by-2 array) with “x(1)” and
“x(2)” to represent x1 and x2 respectively.
•
Do a new figure that creates the contour plot of this function, with
the value of the contours to range between 0 and 80 (for example use:
“V=[0:0.25:2, 3:1:10, 20:10:80]”).
109
•
Call a function with the name: GradDe sce nt that implements the
gradient descent algorithm for minimizing the aforementioned
function. The calling syntax of this function should be:
“[MinPoints, xVals] = GradDe sce nt(fun, x, lr, maxIterNum, tol)”
fun is the function name “@funToMin”, x is a row vector with the
user’s guess (starting value) about the minimum of the function. The
input argument “lr” is the learning parameter a that should be set to
0.1 if not specified by the user. “maxIterNum” is as before the
maximum number of iterations that should be set to 100 if not
specified and “tol” is the tolerance concerning the norm of the
updating component of the point x (stopping criterion) and should be
set to 1e-6 is not specified. The function returns “MinPoints” that if
the algorithm has converged is the point where the function is
minimized, and “xVals” that is an m-by-2 array with the set of the
values of x at each iteration of the algorithm (m is either equal to:
maxIterNum” or a smaller number if the algorithm converges).
This function should call another function with the name: NumerDers
and with the following calling syntax:
“GradsVals = Nume rDe rs(fun,x)”
that takes as input a function and a single coordinate point and
returns the gradient vector at that point. Use the two sided finite
difference method explained before. For the above, use as initial
point: x0=[0 0].
After you have called the function, plot on the contour figure the
algorithm’s trajectory to the minimum found in “xVals”. Call once
more the function with x0=[-1 -2] and add the new trajectory to the
contour figure. Use “lr”=0.25 and “maxIterNum”=200. Use gte xt to
enter a text that indicates the trajectory.
110
•
Call a function with the name: Ne wton that implements the Newton
descent algorithm for minimizing the aforementioned function. The
calling syntax of this function should be:
“[MinPoints,xVals] = Ne wton(fun, x, maxIterNum, tol)”
“fun” is the function name “@funToMin”, x is a row vector with the
user’s guess (starting value) about the minimum of the function.
“maxIterNum” is as before the maximum number of iterations that
should be set to 25 if not specified and tol is the tolerance concerning
the norm of the updating component of the point x (stopping criterion)
and should be set to 1e-6 is not specified. The function returns
“MinPoints” that given that the algorithm has converged, it is the
point where the minimum is located, and “xVals” that is an m-by-2
array with the set of the values of x at each iteration of the algorithm
(m is either equal to “maxIterNum” or a smaller number if the
algorithm converges earlier).
This
function should call another function with the name:
NumerHessian.m and with the following calling syntax:
“HessVals = NumerHessian(fun,x)”
that takes as input a function and a single coordinate point and
returns the Hessian at that point. Use the finite two sided difference
method explained before. To avoid the calculation of a singular
Hessian that cannot be inverted, after saving the Hessian to a square
matrix, set equal to zero all its off diagonal elements. This is a very
useful rule of thumb that helps the algorithm convergence and
robustness. Use x0=[0 0] as initial estimate for the minimum.
After you have called the function, create a new contour figure of the
function and plot on it the algorithm’s trajectory to the minimum
found in “xVals”. Call once more the function with x0=[-1 -2] and add
the new trajectory to the contour figure. Use gte xt to enter a text that
indicates the trajectory.
111
8.3 Portfolio Optimization
Many times, a researcher needs to create a portfolio of securities that for a
desire level of return/profit, it bears the least/minimum risk. The portfolio
optimization problem has been defined since Markowitz (1952) who assumed
that the risk associated with a portfolio can be measured with variance.
The researcher objective is do define via an optimization programming
methodology the weights that each of the alternative assets should have in
the portfolio. By construction, the portfolio return is linear w.r.t to the
weights of the assets and it is given from the following relation:
E( r p ) = W T e
where rp is the weighted average return of the portfolio and E(.) is the
expectation operation. The weight representation of each asset in the
portfolio is given by W and the expected return of each asset is given by e as
follows:
w1
w
W = 2
M
wn
r 1
r
2
and e = E
M
rn
where n is the number of available assets. Contrary, the volatility of the
portfolio w.r.t the weights is a high nonlinear function given by the following
relation:
s P2 = W T OW
where s p represents the weighted average volatility (standard deviation) of
the portfolio, and O is the assets’ variance-covariance matrix:
112
s 11 s 12
s
s 22
O = 21
M
M
s n 1 s n 2
L s 1n
L s 2n
M
M
L s nn
with s ij = cov( ri , r j ) . Additionally, for the portfolio optimization problem, it
is required that the sum of the assets weights should be added to one:
W TNI = 1
with N I to be a column vector with unity elements.
From the above it is obvious that the portfolio optimization problem can be
solved via the minimization of a quadratic volatility function subjected to
linear constrains, one related with the portfolio expected return and another
that assures that all available funds are invested. There are several
convenient mathematical methods for solving this problem. In here, in first
place, it is illustrated the one that is called the method of the Langrangean
multiplier that allows the solution of the general portfolio problem with short
sales with the requirement that the constraints must be in equality form.
When you take the PBA 521: Financial Theory course, you will have to solve
such kind of problems.
The example shown below is copied from the class notes of the above course
offered in 2001 by Professor Spiros Martzoukos. It is the case of three risky
assets without a risk-free rate (it is trivial to generalize it to n risky assets).
The inclusion of the risk free rate is easy; by treating the risk-free rate as a
“risky asset” with zero volatility and zero covariance with all the other assets.
The problem formulation that achieves an expected return equal to R
follows:
min W T O W
wi
s.t.
113
WTe = R
W TNI = 1
and for the case of the three assets in an analytic form:
2
2 2
min w 2A s A
+ wB
s B + wC2 s C2 + 2w A w B s AB + 2w A wC s AC + 2w B wC s BC
wi
s.t.
w A E ( r A ) + w B E ( r B ) + wC E( r C ) = R
w A + w B + wC = 1
Note: If we do not use the first constraint and in the absence of a risk-free
rate we will get the minimum variance portfolio. It is actually advisable to
first get the minimum variance portfolio before we proceed in a real problem.
Then, by changing the level of desire return, we trace points on the efficient
frontier.
To solve this problem, we make two simplifications to the problem. First we
replace everywhere wC with 1 − w A − w B . Second, we rearrange the
constraint:
w A E ( r A ) + w B E ( r B ) + wC E( r C ) = R
to
R − w A E ( r A ) + w B E( r B ) + wC E ( r C ) = 0
and since it equals zero, we multiply it with a constant ? and we get:
?( R − w A E ( r A ) + w B E ( r B ) + wC E ( r C )) = 0
114
Since this equals zero, we add it to the objective function that we want to
minimize without affecting the results. Finally, we minimize the quadratic
function without any constraints. Thus, we have to minimize a function, f (so
it can also be solved with methods that we have seen before). So, after
substitution we have:
2 2
2 2
f = wA
s A + wB
s B + ( 1 − w A + w B ) 2 s C2 + 2w A w B s AB + 2w A ( 1 − w A + w B ) s AC
+ 2w B ( 1 − w A + w B ) s BC + ?( R − w A E ( r A ) − w B E ( r B ) − ( 1 − w A + w B ) E ( rC ))
We need to solve this problem to find the weights of the three assets in the
portfolio. We thus first find the solution to w A , w B and ?. The way to solve
the above problem is now easy. We take the partial derivatives each time in
respect to one of the three unknowns and set them equal to zero, and we will
derive a set of three equations with three unknowns. The first is the partial
derivative of f w.r.t w A , the second w.r.t w B and the third w.r.t the
Langrangean multiplier ?.
The first equation gives:
2
2 w As A
+ ( 2w A + 2w B − 2 ) s C2 + 2wB s AB + ( 2 − 4w A − 2wB ) s AC − 2w B s BC −
?E ( r A ) + ?E( rC ) = 0
The second equation gives:
2
2 wB s B
+ ( 2w A + 2w B − 2) s C2 + 2w A s AB − 2w A s AC + ( 2 − 2w A − 4wB ) s BC −
?E ( r B ) + ?E ( rC ) = 0
The third equation gives:
R − w A E ( r A ) − wB E ( r B ) − ( 1 − w A − w B ) E( rC ) = 0
To work with this case study, assume the following data:
115
r A 0.05
e = E rB = 0.10
rC 0.15
s2
?
O = s BA
s CA
s AB
s ?2
s CB
s AC 0.25 0.15 0.17
s BC = 0.15 0.21 0.09
s C2 0.17 0.09 0.28
Write a script with the name: MeanVarMin.m that will do the following:
•
Saves in a column vector the weights for the solution of the above
mean-variance minimization problem given by:
0.38w A + 0.34wB + 0.10 ? − 0.22 = 0
0.34w A + 0.62w B + 0.05 ? − 0.38 = 0
0.10w A + 0.05w B + 0 − 0.05 = 0
and
wc = 1 − w A − wC
Find its expected return and its standard deviation.
•
Create an m-file with the analytic expression of the function f with the
name: portFun.m with the following syntax:
“f=portFun(x,r,V,R)”
with x to represent a three element vector, x = [ w A , w B , ? ] , r to be
the vector of the assets expected return, V the variance covariance
matrix and R the desire portfolio expected return.
•
Assuming the inexistence of a risk-free rate, create a plot with the
minimum variance opportunity set (current efficient frontier) for
values of R that range between 1% and 40%. The figure should plot
the standard deviation against the portfolio expected return. To do so,
116
change slightly the Ne wton function so that its calling syntax
becomes:
“[MinPoints] = Ne wtonPort(fun, x, r, V, R)”
with r to be the column vector of the assets’ expected returns, V the
assets’ variance-covariance matrix and R the desire expected return.
Similar changes in order to pass the additional arguments should be
done
also
to
NumerDers.m (the new should be named as:
Nume rDe rsPort) and NumerHessian.m (the new should be named as:
Nume rHe ssi anPort). Because the portfolio optimization problem is
actually the minimization of a quadratic function, the Newton descent
algorithm can find its solution with a single iteration. So, alleviate
also the rule of thumb according to which the elements of the Hessian
matrix except the ones of the main diagonal are set to zero. Use the
origin (0, 0, 0) as an initial point.
•
Add a risk free asset with expected return 1%, find and plot the
efficient
frontier.
Create
a
new
m-file
with
the
name:
portFunRiskFree.m that includes the new expression of f after the
inclusion of risk-free rate (hint: find which components are zerovalued and ignore them). Create a third figure that combines the two
previous ones. If you are familiar with investment theory, you can
view various interesting components (e.g. two fund separation
theorem, capital market line, etc).
117
References
[1] Ela Pekalska, Marjolein van der Glas, (2001), “Introduction to MATLAB”,
Pattern Recognition Group, Faculty of Applied Sciences, Delft University
Technology.
[2] MATLAB® Release 13 Online Help.
[3] Bharadia M. A. J., Christofides N, and Salkin G. R., (1995), “Computing
the Black and Scholes Implied Volatility”, Advances in Futures and Options
Research, Vol. 8, pp. 15-29.
[4] Miranda M. and Fackler P., (2002), Applied Computational Economics and
Finance, Massachusetts Institute of Technology.
[5] Bertsekas D., (1999), Nonlinear Programming, 2nd Edition, Athena
Scientific.
[6] Griffiths D., (2001), “An Introduction to Matlab: Version 2.2”, Department
of Mathematics, The University Dundee DD1 4HN.
[7] Silvestrov D., and Malyarenko A., (2001), “An Introduction to Financial
Mathematics With MATLAB”, Malardalen University.
[8] Chandler G., (2000), “Introduction to Matlab”, Mathematics Department,
The University of Queensland.
[9] Ferrari S., (2000), “Tutorials in Robotics and Intelligent Systems: Part IV.
Introduction to MATLAB Optimization Toolbox”, Department of Mechanical
and Aerospace Engineering, Princeton Unive rsity.
118